Next: 18.0.0.1 問 Up: FreeFem++ ノート Previous: 17 ARGV
菊地 [4] に載っている Poisson 方程式の例題
| (1) | |
| (2) | |
| (3) | 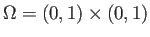 |
| kikuchi-poisson.edp |
// kikuchi-poisson.edp
int Gamma1=1, Gamma2=2;
border Gamma10(t=0,1) { x=0; y=1-t; label=Gamma1; }
border Gamma11(t=0,1) { x=t; y=0; label=Gamma1; }
border Gamma20(t=0,1) { x=1; y=t; label=Gamma2; }
border Gamma21(t=0,1) { x=1-t; y=1; label=Gamma2; }
int m=10;
mesh Th = buildmesh(Gamma10(m)+Gamma11(m)+Gamma20(m)+Gamma21(m));
plot(Th, wait=1,ps="Th.eps");
savemesh(Th,"Th.msh"); // optional
fespace Vh(Th,P1);
Vh u,v;
func f=1;
func g1=0;
func g2=0;
solve Poisson(u,v) =
int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
-int2d(Th)(f*v)
-int1d(Th,Gamma2)(g2*v)
+on(Gamma1,u=g1);
plot(u,ps="contour.eps");
|