


Next: B..1.0.2 (2) の証明
Up: B..1 スツルムの定理
Previous: B..1 スツルムの定理
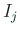 内のある部分区間
内のある部分区間 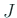 において、すべての多項式
において、すべての多項式
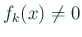 とすると、
とすると、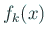 の符号は
の符号は 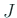 で一定であるので (中間値の定理から、
符号が変化するには 0
にならないといけない)、
で一定であるので (中間値の定理から、
符号が変化するには 0
にならないといけない)、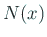 の値は変化しないこ
とが分かる。
の値は変化しないこ
とが分かる。
そこで、ある多項式 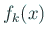 の解
の解
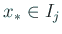 を通過した場合を考える。
Strum 列の条件から
を通過した場合を考える。
Strum 列の条件から 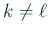 ,
, 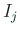 の取り方から
の取り方から 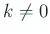 であるから、
であるから、
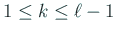 である。Strum 列の条件 (2) から
である。Strum 列の条件 (2) から
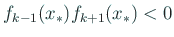 であるが、連続性から
であるが、連続性から 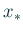 の十分小さな近傍
の十分小さな近傍 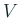 を
取れば、そこで
を
取れば、そこで
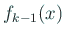 と
と
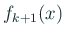 は定符号となり、
は定符号となり、
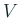 上で
上で
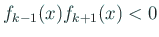 がなりたつ。
それゆえ、列
がなりたつ。
それゆえ、列
の部分列
の符号については次の二つのいずれか一方だけしか起こらない。
(a)
(b)
それゆえ、(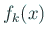 の符号が何であっても) 任意の
の符号が何であっても) 任意の 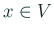 について、部分列
について、部分列
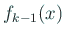 ,
, 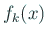 ,
,
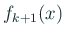 における符号の変化は
における符号の変化は 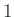 として
として
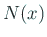 の値に算入される。
これから
の値に算入される。
これから 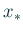 の十分小さな近傍で
の十分小さな近傍で 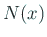 の値に
変化はないことが分かる。
ゆえに
の値に
変化はないことが分かる。
ゆえに 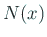 は
は 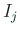 上で定数である。
上で定数である。



Next: B..1.0.2 (2) の証明
Up: B..1 スツルムの定理
Previous: B..1 スツルムの定理
桂田 祐史
2015-12-22
![]() の解
の解
![]() を通過した場合を考える。
Strum 列の条件から
を通過した場合を考える。
Strum 列の条件から ![]() ,
, ![]() の取り方から
の取り方から ![]() であるから、
であるから、
![]() である。Strum 列の条件 (2) から
である。Strum 列の条件 (2) から
![]() であるが、連続性から
であるが、連続性から ![]() の十分小さな近傍
の十分小さな近傍 ![]() を
取れば、そこで
を
取れば、そこで
![]() と
と
![]() は定符号となり、
は定符号となり、
![]() 上で
上で
![]() がなりたつ。
それゆえ、列
がなりたつ。
それゆえ、列
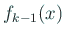
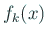
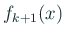
上

上

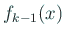
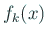
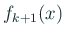
上

上
