


Next: B..1.0.1 (1) の証明
Up: B. Strum の方法
Previous: B. Strum の方法

この定理によって、区間 ![$ [a,b]$](img252.gif) 内に存在する
内に存在する 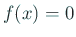 の解を数を知るこ
とができるが、二分探索の技法と組み合わせることで、解が存在する区間を好き
なだけ小さくすることが出来、その区間内の適当な点を解の近似値として採用す
るという近似解法ができる。これをStrum の方法と呼ぶ。
の解を数を知るこ
とができるが、二分探索の技法と組み合わせることで、解が存在する区間を好き
なだけ小さくすることが出来、その区間内の適当な点を解の近似値として採用す
るという近似解法ができる。これをStrum の方法と呼ぶ。
証明.
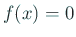
の解の個数は有限個である。そのうち
![$ [a,b]$](img252.gif)
に含まれるものを大き
さの順に並べて
とする。
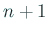
個の区間
の和集合において (
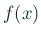
は 0
とならないので)
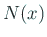
が定義できる。
以下では
- (1)
- 各区間
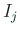 において
において 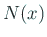 は定数である:
は定数である:
- (2)
-
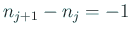 (
(
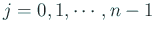 )
)
であることを証明する (この二つから容易に
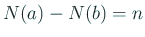
が導かれる)。

Subsections



Next: B..1.0.1 (1) の証明
Up: B. Strum の方法
Previous: B. Strum の方法
桂田 祐史
2015-12-22
![\begin{jdefinition}[Strum列]\upshape
$[a,b]$\ を $\R$\ の区間とすると�...
...�て $f(x_0)=0$\ ならば $f'(x_0)f_1(x_0)>0$.
\end{enumerate}\end{jdefinition}](img381.gif)
![\begin{jdefinition}[Strum列]\upshape
$[a,b]$\ を $\R$\ の区間とすると�...
...�て $f(x_0)=0$\ ならば $f'(x_0)f_1(x_0)>0$.
\end{enumerate}\end{jdefinition}](img381.gif)
![\begin{jdefinition}[符号変化の回数]\upshape
実係数多項式の列 $f(...
...��号
変化したと数えることにする。
\end{itemize}\end{jdefinition}](img382.gif)
![]()
![\begin{jtheorem}[Strum]\upshape
実係数多項式の列 $f(x)=f_0(x)$, $f_1(x)...
...�� $[a,b]$\ における解の個数は $N(a)-N(b)$\ である。
\end{jtheorem}](img384.gif)
![]() 内に存在する
内に存在する ![]() の解を数を知るこ
とができるが、二分探索の技法と組み合わせることで、解が存在する区間を好き
なだけ小さくすることが出来、その区間内の適当な点を解の近似値として採用す
るという近似解法ができる。これをStrum の方法と呼ぶ。
の解を数を知るこ
とができるが、二分探索の技法と組み合わせることで、解が存在する区間を好き
なだけ小さくすることが出来、その区間内の適当な点を解の近似値として採用す
るという近似解法ができる。これをStrum の方法と呼ぶ。
![]()