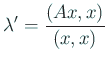


Next: 2.5 逆反復法
Up: 2 解法についての概観
Previous: 2.3.0.1 大雑把な説明
誤差がなければ、
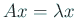 の適当な(
の適当な(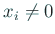 となる
となる 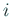 に
対する)成分に対応する方程式
に
対する)成分に対応する方程式
の両辺を 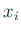 で割れば
で割れば 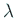 が求まるが、
が求まるが、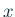 が近似的な固有ベクト
ルでしかない場合には、
以下に解説する Rayleigh3 商を用いる方法の方が良い。
が近似的な固有ベクト
ルでしかない場合には、
以下に解説する Rayleigh3 商を用いる方法の方が良い。
証明.

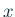 を
を 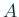 の近似固有ベクトルとする時、Rayleigh 商
の近似固有ベクトルとする時、Rayleigh 商
は 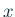 に対応する固有値の良い近似になる。粗く言って
に対応する固有値の良い近似になる。粗く言って
が成り立つ。詳しくは次の命題を見よ。
証明.
省略。一松 [
7] あるいは [
3] を見よ。




Next: 2.5 逆反復法
Up: 2 解法についての概観
Previous: 2.3.0.1 大雑把な説明
桂田 祐史
2015-12-22
![]() の適当な(
の適当な(![]() となる
となる ![]() に
対する)成分に対応する方程式
に
対する)成分に対応する方程式
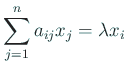
![\begin{jdefinition}[Rayleigh商]\upshape
$N$\ 次正方行列 $A$\ と、$x\in\...
...� $A$\ の $x$\ に対する \textbf{Rayleigh 商}という。
\end{jdefinition}](img78.gif)
![$\displaystyle \Vert x\Vert^2
\left[
\lambda-\frac{(x,Ax)}{\Vert x\Vert^2}
\r...
... x\Vert^2}
\right]
+\Vert Ax\Vert^2-\frac{\vert(x,Ax)\vert^2}{\Vert x\Vert^2}$](img83.gif)
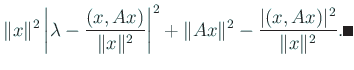
![]() を
を ![]() の近似固有ベクトルとする時、Rayleigh 商
の近似固有ベクトルとする時、Rayleigh 商