


Next: 6.5.0.3 一発でうまくやることはあきらめて
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5.0.1 任意の に対して となる場合
一方 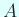 の最小多項式の次数
の最小多項式の次数 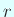 が
が 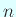 に等しい場合は、
に等しい場合は、
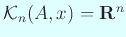 をみたす
をみたす 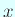 が存在することがわかるが
(証明?)、実際にどうやってそのような
が存在することがわかるが
(証明?)、実際にどうやってそのような 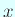 を見つけるか、
あまり簡単ではない。
極端な話、
を見つけるか、
あまり簡単ではない。
極端な話、
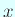 を
を 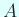 の固有ベクトルに選んでしまった場合は
の固有ベクトルに選んでしまった場合は
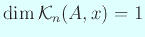 であり、Lanczos 法の反復は
であり、Lanczos 法の反復は 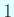 ステップで止まってしまう。
もっと極端な話、
ステップで止まってしまう。
もっと極端な話、
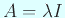 の場合、
いかなる
の場合、
いかなる 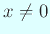 も
も 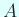 の固有ベクトルになってしまう。
おそらく最小多項式の次数が
の固有ベクトルになってしまう。
おそらく最小多項式の次数が 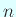 である場合は、
generic に
である場合は、
generic に
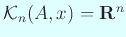 となるのであろうが…
となるのであろうが…



Next: 6.5.0.3 一発でうまくやることはあきらめて
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5.0.1 任意の に対して となる場合
桂田 祐史
2015-12-22