![\begin{jlemma}[実行列の要素の平方和]\upshape
$A=(a_{ij})\in\R^{n\time...
...math}
\sum_{i,j=1}^n {a_{ij}}^2={\rm tr} (A^T A).
\end{displaymath}\end{jlemma}](img190.png)
誰だったか忘れたが (戸川先生?)、 Jacobi 法をモグラ叩きに例えた人がいる。 これはなかなかイメージが湧いてきて良いと思う。
![\begin{jlemma}[実行列の要素の平方和]\upshape
$A=(a_{ij})\in\R^{n\time...
...math}
\sum_{i,j=1}^n {a_{ij}}^2={\rm tr} (A^T A).
\end{displaymath}\end{jlemma}](img190.png)
|
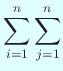 | |||
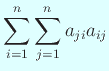 | |||
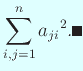 |
実行列 ![]() を実直交行列
を実直交行列 ![]() で相似変換した
で相似変換した ![]() について、
について、
となるが、 良く知られた公式
であるから、
つまり
![\begin{jlemma}[Jacobi のもぐらたたき一発分の効果]\upshape
$n\in\N$...
...sum_{i\ne j}{b_{ii}}^2+2{a_{pq}}^2.
\end{displaymath}\end{enumerate}\end{jlemma}](img205.png)
|
![\begin{jtheorem}[古典 Jacobi法の原理]\upshape
$A$ を実対称行列と�...
..._k
\end{displaymath}の各列が固有ベクトルを与える。
\end{jtheorem}](img206.png)
|
この定理に基づき、![]() が十分対角行列に近づいたときに計算を打ち切り、
が十分対角行列に近づいたときに計算を打ち切り、
![]() の近似固有値として
の近似固有値として
![]() ,
, ![]() ,
,
![]() , それらに属する近似固有ベクトルとして
, それらに属する近似固有ベクトルとして
![]() の各列を採用する。これを古典 Jacobi 法と呼ぶ。
の各列を採用する。これを古典 Jacobi 法と呼ぶ。
有限ステップで停止したときの誤差評価として、次の定理がある。
![\begin{jtheorem}[近似固有値を非対角要素の平方和で評価]\upshape...
...ath}
F^{(k+N)}\le C (F^{(k)})^2.
\end{displaymath}\end{enumerate}\end{jtheorem}](img210.png)
|
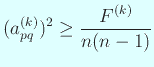
であり、
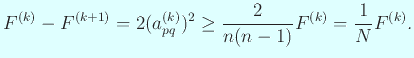
(3) については省略。
絶対値最大の要素の探索はかなり手間がかかる (計算量が大きくなる) ので、
色々な変種が考えられている。
ある「しきい閾値」
![]() と選び、
と選び、
![]() なる
なる
![]() に対して回転を施す
閾値 Jacobi 法や、
に対して回転を施す
閾値 Jacobi 法や、
|
![\begin{jremark}[Jacobi 法の評判]\upshape
Jacobi 法の評判をいくつか...
...�再評価されはじめているのは興味深い。
\end{quote}\end{jremark}](img218.png)