Next: A..3 Bessel ťĖĘśēį„ĀģśÄߍ≥™ Up: A..2 Bessel „ĀģŚĺģŚąÜśĖĻÁ®čŚľŹ Previous: A..2.2 Frobenius „ĀģśĖĻś≥ē„ĀßŤß£„āíśĪā„āĀ„āč
![]() „Āß„Āā„āč„Ā®„Āć„ÄĀ
„Āß„Āā„āč„Ā®„Āć„ÄĀ
![]() ,
,
![]() „ĀĮ1ś¨°Áč¨Áęč„Āß„Āā„āč
(„Āó„Āü„ĀĆ„Ā£„Ā¶ (3) „ĀģŤß£„ĀģŚüļśú¨Á≥Ľ„Āę„Ā™„āč)„Äā
„Āď„āĆ„ĀĮšł°ŤÄÖ„ĀģÁīöśēįŤ°®Á§ļ„ā퍶č„Ā¶„ÄĀ
„ĀĮ1ś¨°Áč¨Áęč„Āß„Āā„āč
(„Āó„Āü„ĀĆ„Ā£„Ā¶ (3) „ĀģŤß£„ĀģŚüļśú¨Á≥Ľ„Āę„Ā™„āč)„Äā
„Āď„āĆ„ĀĮšł°ŤÄÖ„ĀģÁīöśēįŤ°®Á§ļ„ā퍶č„Ā¶„ÄĀ
![]() „Āģ„Ā®„Āć„ĀģŚĘóŚ§ßŚļ¶„āíŤÄÉ„Āą„Ā¶„āāŚģĻśėď„Āꍮľśėé„Āß„Āć„āč„ĀĆ„ÄĀ
ś¨°„ĀģŤ£úť°Ć„Āč„āČ„āāŚąÜ„Āč„āč„Äā
„Āģ„Ā®„Āć„ĀģŚĘóŚ§ßŚļ¶„āíŤÄÉ„Āą„Ā¶„āāŚģĻśėď„Āꍮľśėé„Āß„Āć„āč„ĀĆ„ÄĀ
ś¨°„ĀģŤ£úť°Ć„Āč„āČ„āāŚąÜ„Āč„āč„Äā

|

„É≠„É≥„āĻ„ā≠„āĘ„É≥„ĀģÁ≠ČŚľŹ„Āč„āČśÉ≥ŚÉŹ„Āß„Āć„āč„Āď„Ā®„Ā†„ĀĆ„ÄĀ
![]() „Āģ„Ā®„Āć
„Āģ„Ā®„Āć ![]() ,
,
![]() „ĀĮ1ś¨°ŚĺďŚĪě„Āę„Ā™„āč„Äā
„Āď„āĆ„ĀĮŚģĻśėď„ĀęÁĘļ„Āč„āĀ„āČ„āĆ„āčťĖĘšŅā
„ĀĮ1ś¨°ŚĺďŚĪě„Āę„Ā™„āč„Äā
„Āď„āĆ„ĀĮŚģĻśėď„ĀęÁĘļ„Āč„āĀ„āČ„āĆ„āčťĖĘšŅā
„Āč„āČśėé„āČ„Āč„Āß„Āā„āč„Äā
„Āē„Ā¶„ÄĀ
„ĀĄ„āą„ĀĄ„āąÁ¨¨šļĆÁ®ģ„Éô„ÉÉ„āĽ„ÉęťĖĘśēį („Éé„ā§„Éě„É≥ťĖĘśēį„Ā®„āā„ĀĄ„ĀÜ) ![]() „āíŚįéŚÖ•„Āó„āą„ĀÜ„Äā
„āíŚįéŚÖ•„Āó„āą„ĀÜ„Äā
„Āĺ„Āö
![]() „ĀģŚ†īŚźą„Āę
„ĀģŚ†īŚźą„Āę
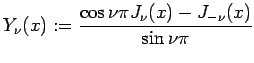
„Ā®„Āä„ĀŹ„Äā „Āď„āĆ„ĀĮ
„Āē„āČ„Āę ![]() „ĀęŚĮĺ„Āó„Ā¶ŚļÉÁĺ©šłÄśßėŚŹéśĚüś•Ķťôź
„ĀęŚĮĺ„Āó„Ā¶ŚļÉÁĺ©šłÄśßėŚŹéśĚüś•Ķťôź
„ĀĆŚ≠ėŚú®„Āô„āč„Äā„ĀĚ„Āď„Āß
„Ā®„Āä„ĀŹ„Ā®„ÄĀ „Āď„āĆ„āā (3) „ĀģŤß£„Āß„Āā„āč„ĀĆ„ÄĀ (5) „āą„āä8
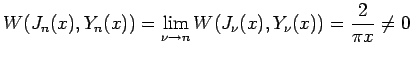
„Āß„Āā„āč„Āč„āČ„ÄĀ
šĽ•šłä„āí„Āĺ„Ā®„āĀ„āč„Ā®ś¨°„ĀģŚģöÁźÜ„ĀĆŚĺó„āČ„āĆ„āč„Äā
|
|
ś°āÁĒį Á•źŚŹ≤