... の値を求める方法について論じる1
多次元の数値積分については、 次元が低い場合は優良格子点法、次元が高い場合はモンテ・カルロ法が有効で、 学ぶ価値は高いが、複素関数論の守備範囲ではないと考えられるので省略する。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Bessel関数の積分表示2
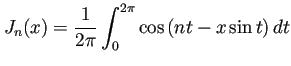$ J_n(x) =\dsp\frac{1}{2\pi}\int_0^{2\pi}\cos\left(nt-x\sin t\right)\D t$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... ほぼ使用している処理系の最高精度に到達している3
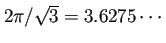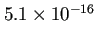最近のパソコンの C 言語処理系では、 浮動小数点数は、IEEE 754 という規格に従っている。 double 型のデータの内部表現は、 仮数部が2進法で53桁で、10進法に換算すると、16桁弱に相当する。 $ 2\pi/\sqrt{3}=3.6275\cdots$ なので、 誤差が $ 5.1\times 10^{-16}$ ということは、 ほぼ16桁正しいことになる。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... その後は、分割を細かくしても精度は上がらないが4
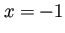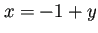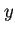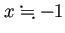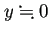その原因を「桁落ち (cancellation of siginificant digits) が起こるせい」と言う人もいる。 ある意味では正しいが、誤解を産みやすい説x明である。 例えば $ x=-1$ 付近の値を計算する場合に、 $ x=-1+y$ で導入した変数 $ y$ を使うことにすると、 $ x\kinji -1$ であるから $ y\kinji 0$. 浮動小数点数では、 0 に近いところは非常にきめ細かになっていることに注意する。 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
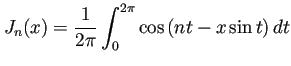
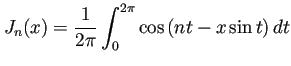