4.3 数値例

前節で中点公式、台形公式、Simpson 公式でまともに解けなかった

$$I=\int_{-1}^1\sqrt{1-x^2 }\;\D x \quad\left(=\frac{\pi}{2}\right)$$

を $\varphi_1$ を用いる DE 公式 $I_{h,N}$ で近似してみる。

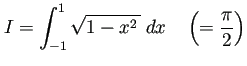
$h=1$, $N=4$ から始め、$h$ を半分、$N$を2倍にしていく。

example6 の結果 (前半)

% cc -o example6 example6.c
% ./example6
test1 (sqrt(1-x^2) の積分)
h=1.000000, N=   4, I_hN=       1.7125198292703636, I_hN-I=1.417235e-01
h=0.500000, N=   8, I_hN=       1.5709101233831166, I_hN-I=1.137966e-04
h=0.250000, N=  16, I_hN=       1.5707963267997540, I_hN-I=4.857448e-12
h=0.125000, N=  32, I_hN=       1.5707963267948970, I_hN-I=4.440892e-16
h=0.062500, N=  64, I_hN=       1.5707963267948968, I_hN-I=2.220446e-16

(後略)

驚くべきことに、 $h=\frac{1}{8}$, $N=24$で誤差がほぼ $10^{-16}$ 程度になっている。 $x=\pm 1$ にあった特異性は、変数変換により消えてしまった。

それどころか、もっと特異性の強い ($x=\pm 1$ で分母が 0 ！！)

$$I=\int_{-1}^1 \frac{\Dx}{\sqrt{1-x^2}}=\pi$$

に対しても、計算が可能である。

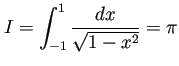
test2 (1/sqrt(1-x^2) の積分)
h=1.000000, N=   4, I_hN=       3.1435079763395439, I_hN-I=1.915323e-03
h=0.500000, N=   8, I_hN=       3.1415926717394895, I_hN-I=1.814970e-08
h=0.250000, N=  16, I_hN=       3.1415926194518016, I_hN-I=-3.413799e-08
h=0.125000, N=  32, I_hN=       3.1415926318228000, I_hN-I=-2.176699e-08
h=0.062500, N=  64, I_hN=       3.1415926343278699, I_hN-I=-1.926192e-08
h=0.031250, N= 128, I_hN=       3.1415926326210668, I_hN-I=-2.096873e-08
h=0.015625, N= 256, I_hN=       3.1415926323669527, I_hN-I=-2.122284e-08
h=0.007812, N= 512, I_hN=       3.1415926327540080, I_hN-I=-2.083579e-08
h=0.003906, N=1024, I_hN=       3.1415926312582507, I_hN-I=-2.233154e-08
h=0.001953, N=2048, I_hN=       3.1415926319069589, I_hN-I=-2.168283e-08
%

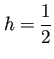$h=\dfrac{1}{2}$, $N=8$ で誤差が $10^{-8}$ 程度になっている。 その後は、分割を細かくしても精度は上がらないが ⁴、 $x=\pm 1$ の付近で $\sqrt{1-x^2}$ が精度良く計算出来ないためで、 適切に対策 ($x=\pm 1$ が原点に来るような変数変換) すれば解決できる。 詳細な説明は省略するがサンプル・プログラムとその結果は紹介しておく。

example6kai の結果 (後半)

% cc -o example6kai example6kai.c
% ./example6kai

(中略)

test2 (1/sqrt(1-x^2) の (-1,1) での積分)
h=1.000000, N=   4, I_hN=       3.1435079789309328, I_hN-I=1.915325e-03
h=0.500000, N=   8, I_hN=       3.1415926733057051, I_hN-I=1.971591e-08
h=0.250000, N=  16, I_hN=       3.1415926535897940, I_hN-I=8.881784e-16
h=0.125000, N=  32, I_hN=       3.1415926535897940, I_hN-I=8.881784e-16

(以下略)

$h=\frac{1}{4}$, $N=16$ で誤差が $10^{-16}$ 程度になっている。