1 はじめに

定積分の値を数値計算で求めることを数値積分という。

微分の計算はある意味で簡単 (導関数が分かっている関数を組み合わせて作った関数の導関数は求められる) であるが、積分の計算は難しいことが多い。

そこで定積分の値を数値計算で求めることが必要になる。 この文書では1変数関数の積分

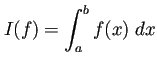$$I(f)=\int_a^b f(x)\;\Dx$$ (1)

の値を求める方法について論じる¹。

特別の $f$ に対して $I(f)$ を計算するのではなく、 ある程度広い範囲の $f$ について、 共通のやり方で $I(f)$ を計算する方法を考察する。

応用上現れる近似公式 (数値積分公式) は 、ほとんどが次の形をしている。

$$I_n(f)=\sum_{k=1}^n A_k f(x_k).$$ (2)

ここで $x_k$ は $[a,b]$ 内から選んだ相異なる点で、 標本点 (sample point) と呼ばれる。 また $A_k$ は重み (weight) と呼ばれる。

この文書で取り上げる

(a)

補間型数値積分公式

(b)

二重指数関数型数値積分公式 (double exponential formula)

はいずれも (2) の形をしている。