10.2 大石-Rump, 1999年から2000年

1999年のテキスト [39] では、 §5 が「連立一次方程式の精度保証」となっている。 §5.1「点行列」では、 基礎とするのは、$Ax=b$ を解く際に、$A$ の近似行列$R$があったとして、 $G:=RA-I$ とおくとき、 $\left\Vert G\right\Vert _\infty<1$ が満たされるならば、

$$\left\Vert A^{-1}\right\Vert _\infty\le \frac{\left\Vert R\right... ...\infty\left\Vert Ac-b\right\Vert _\infty} {1-\left\Vert G\right\Vert _\infty}$$

成り立つ、という定理である ($c$ は任意の元だと思う)。 近似逆行列 $R$, 残差 $Ac-b$ ($c$ が近似解), $G$ のノルム $\left\Vert R\right\Vert _\infty$, $\left\Vert Ac-b\right\Vert _\infty$, $\left\Vert G\right\Vert _\infty$ の評価を行う必要がある。

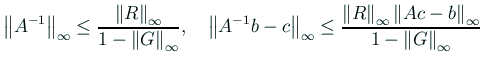
プログラムA

setround(down);
     $\underline{G}=R A-I$;
     $\underline{r}=Ac-b$;
setround(up);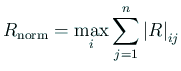
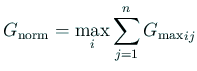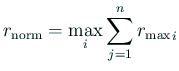     $\overline{G}=R A-I$;
     $\overline{r}=Ac-b$;

それと

プログラムB

     $G_{\text{max}}=\max\left\{\left\vert\underline{G}\right\vert, \left\vert\overline{G}\right\vert\right\}$;
     $r_$max$=\max \left\{ \left\vert\underline{r}\right\vert,\left\vert\overline{r}\right\vert \right\}$;
setround(up);
     $R_{\text{norm}}=\dsp\max_{i}\sum_{j=1}^n\left\vert R\right\vert _{ij}$;
     $G_{\text{norm}}=\dsp\max_{i}\sum_{j=1}^n{G_{\max}}_{ij}$;
     $r_{\text{norm}}=\dsp\max_{i}\sum_{j=1}^n {r_{\max}}_{i}$;
setround(down);
     $D=1-G_{\text{norm}}$;
if ($D>0$) {
    setround(up);
     $A_{\text{in}}=R_{\text{norm}}/D$;
     $s=A_{\text{in}} r_{\text{norm}}$;
}
     else print("false");

こうして計算された $A_{\text{in}}$, $s$ は、 それぞれ $\left\Vert A^{-1}\right\Vert _\infty\le A_{\text{in}}$, $\left\Vert A^{-1}b-c\right\Vert\le s$ の評価となる。すなわち

$$\left\Vert A^{-1}\right\Vert _\infty\le A_{\text{in}}, \quad \left\Vert A^{-1}b-c\right\Vert\le s$$

を満たす。 さらに区間行列を係数行列に持つ連立一次方程式の精度保証、 ヤコビ法についても言及している。

この§5の内容はどこから来たのかな？

次の大石 [40] はかなりきちんと書かれている。 まず、上に紹介した定理について 「この定理は古くから知られているものである。」 と述べている。さらに「プログラムA」,「プログラムB」を擬似コードでなく、 MATLAB プログラムで示している (p. 36)。

大石 [40] p. 36

% linear1.m
clear
N=200
formatlong
A=rand(N);   % A is an NxN random matrix
b=rand(N,1); % b is a random N-vector
R=inv(A);    % R is the inverse of A
x=R*b;
down;
Gd=abs(R*A-eye(N)); % eye(N) is the identity matrix
rd=abs(A*x-b);
up;
Gu=abs(R*A-eye(N));
ru=abs(A*x-b);
ru=max(rd,ru);
Gu=max(Gd,Gu);
R_norm=norm(R,inf); % maximum norm
G_norm=norm(Gu,inf);
r_norm=norm(ru,inf);
down;
D=1-G_norm;
if D>0
  up;
  A_inv=R_norm/D
  error=A_inv*r_norm
else
  disp('false')
end

[40]の§2.2.4「成分毎評価」では、 「$\tilde x$を近似解とし、$x^\ast$ を真の解とする。 誤差 $e=x^\ast-\tilde x$をノルム $\left\Vert e\right\Vert$で評価する 方法をより精度のよい評価法に改良する方向として、 $\left\Vert e\right\Vert$を評価することが考えられる。ただし

$$\left\vert e\right\vert= \left( \left\vert e_1\right\vert, \left\vert e_2\right\vert, \cdots, \left\vert e_n\right\vert \right)$$

である。この方向の研究は、コラッツ、シュレーダー、占部などによって開拓され、 山本哲郎は次の使いやすい定理を示した。」 と書いて、Yamamoto [41] の定理を証明付きで紹介し、 さらには MATLAB プログラムを示している。

大石 [40] p. 42

% Cw1.m
clear
N=20
A=rand(N);
b=rand(N,1);
R=inv(A);
X=R*b;
down;
Gd=abs(R*A-eye(N));
rd=A*x-b;
up;
Gu=abs(R*A-eye(N));
ru=A*x-b;
center=(ru+rd)/2;
radius=center-rd;
ru=max(rd,ru);
Gu=max(Gd,Gu);
R_norm=norm(R,inf);
G_norm=norm(Gu,inf);
Rru=abs(R*center+abs(R)*radius);
down;
D=1-G_norm;
if D>0
  up;
  Rru=max(Rrd,Rru);
  Rr_norm=norm(Rru,inf);
  error=Rr_norm/D;
  kappa=Gu*ones(N,1);
  error2=Rru+(error*kappa)
  cwerror=max(error2)
else
  disp('false')
end

§2.3「LU分解を用いて高速精度保証」は、 大石先生のオリジナルなのだろうか？ (これは次の大石[42]を読むと明らかになる。) ここはきちんと解読して説明を書いておきたい。

§2.4「コレスキー分解」では、 コレスキー分解の定義と計算手順を書いた後に 「正定値対称行列に対して、 以上のような分解法を用いれば、 近似解を求めるのも精度保証をするのも、 普通のLU分解をするのと比べ2倍高速になることはいうまでもないであろう。」 で締めている。 礒野君にはその「いうまでもないこと」をきちんとやってもらった (これは §2.3 の解読をしたい、というねらいがあったのだけど、 「説明を書」く方はサボっているわけだ)。

§2.5「スパース行列手法」は、 帯行列をLU分解すると、 帯行列になるので、§2.3 のやり方がそのままうまく行く、 という注意を書いてある。 「例えば、対角要素が$-2$で副角要素が$1$である3重対角行列を スパース行列処方で解くMATLABのプログラムは、係数行列を

  e=onex(N,1);
  A=spdiags([e -2*e e],-1:1,N,N);

と書き換えるだけで得られる。これは、 もちろん完全なチューンアップというわけではないが、 それでも例2.2のプログラムで入力をこのように変更して、 スパース行列手法で解かせると、 1000元の連立一次方程式を例2.2と同じ コンピューターで5秒で, 2000元では27秒で解ける。」と締めている。

日本シミュレーション学会誌2000年9月号に 大石[42] を発表している。

「しかし、 単純のプログラムを作成すると精度保証に数値解を得る計算時間の9倍の手間がかかる。 これを、後退誤差解析の最新の成果を利用して、改良すると、 精度保証の計算時間を $1/9$倍 にできることを著者は Rump との共同研究で示した。 すなわち、 精度保証に要する計算時間が数値解を計算する手間と同じであることが示された。

つまり大石[42]に書かれている内容は、 S. M. Rump との共同研究の成果である、ということらしい。 論文で言うと Oish-Rump [12]) ということか？ (ここまでの大石先生の突進ぶりからすると、 2年後の発表というのは遅く感じるけれど、 これは論文誌側の事情なのかな。)

「Linux数値計算ツール」という風変わりなタイトルの大石 [40] は、MATLAB でなくても、 そういう計算は出来る、ということを見せたかったのだろうか。 Otcave, Scilab, LAPACK, Calc など出て来るのは面白いけれど、 話はそれほど深くはない。 あ、Calc の修正は柏木先生なんだ。ほほー。

大石 [43] は固有値の精度保証の話だ。 これもそのうち解読しておかないと。