


Next: E.3 �$B%W%m%0%i%`�(B
Up: E.2 �$BDI2C$NLdBj�(B
Previous: E.2.0.0.2 �$BLdBj�(B8-5
3 �$B$J!"$$$o$f$k�(B Lorenz Model
�$B$K=i4|>r7o�(B
�$B$r2]$7$?=i4|CMLdBj$r2r$$$F!"Aj?^$rIA$1!#$3$3$G�(B 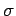 ,
, 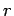 ,
, 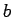 �$B$O@5�(B
�$BDj?t!#$3$N%Q%i%a!<%?$NA*Dj$O=EMW$J0UL#$r;}$D$,!"�(B �$B$^$:$O�(B Lorenz �$B$,Nc�(B
�$B$H$7$FA*$s$@$H$$$&CM!J�(B
�$B$O@5�(B
�$BDj?t!#$3$N%Q%i%a!<%?$NA*Dj$O=EMW$J0UL#$r;}$D$,!"�(B �$B$^$:$O�(B Lorenz �$B$,Nc�(B
�$B$H$7$FA*$s$@$H$$$&CM!J�(B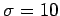 ,
, 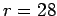 ,
, 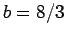 �$B!K$r;n$7$F$_$h!#�(B
�$B!K$r;n$7$F$_$h!#�(B



Next: E.3 �$B%W%m%0%i%`�(B
Up: E.2 �$BDI2C$NLdBj�(B
Previous: E.2.0.0.2 �$BLdBj�(B8-5
Masashi Katsurada
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B28�$BF|�(B