Next: 9.4.0.1 練習問題 (偏微分方程式を勉強する人向け) Up: 9 テクニック集 Previous: 9.3 細かい技 (凡例、ラベル等)
スクリプトを reread することによって、簡単なアニメーションが実現出来ます。
偏微分方程式論で有名な熱方程式の基本解
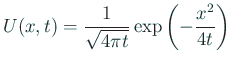
| anim.gp |
plot [-10:10] [0:1] u(x,t) t=t+dt if (t<Tmax) reread |
gnuplot> u(x,t)=exp(-x*x/(4*t))/sqrt(4*pi*t) gnuplot> t=0.1 gnuplot> Tmax=5 gnuplot> dt=0.01 gnuplot> load "anim.gp" |
ここでは静止画で我慢。
(工夫すれば GIF アニメーションとか作れそうですね。 … set term gif animate として set output "なんとか.gif" とするだけでした。)
(2017/11/7 加筆) gnuplot ver 4.6 から、do for という新しい構文が導入されて、 それを使うと、次のように書ける。
Tmax=5.0
Nmax=500
dt=Tmax/Nmax
u(x,t)=exp(-x*x/(4*t))/sqrt(4*pi*t)
do for [i=1:Nmax] {
t=i*dt
plot [-10:10] [0:1] u(x,t)
}
(最初 Tmax=5 としたら、
dt が 0 になってハマってしまった。)
|