Next: 24 爆発問題 Up: 23.3 数値等角写像で Green 関数を近似計算してみる Previous: 23.3 数値等角写像で Green 関数を近似計算してみる
領域 ![]() における
における
![]() の Green 関数というのは、
導体で囲まれた領域内の任意の点
の Green 関数というのは、
導体で囲まれた領域内の任意の点 ![]() に単位点電荷をおいたときの、
任意の点
に単位点電荷をおいたときの、
任意の点 ![]() における静電位を与える関数
における静電位を与える関数 ![]() のことである。
式で表現すると、
のことである。
式で表現すると、![]() は
は
という条件を満たすような関数ということになる。
Green 関数は偏微分方程式の入門書にもしばしば載っている基本的な概念であるが、
具体的に求められるのは非常に限られた場合
(テキストに載っているのは円盤領域とか半平面とか)
しかない。
普通出来るのは、Green 関数の存在証明で、
それを使って (ある意味で) 抽象的な議論を行うためのもの、
というように私 (桂田) は理解していた。
例えば一般の非同次項 ![]() を持つ Poisson 方程式の境界値問題
を持つ Poisson 方程式の境界値問題
の解
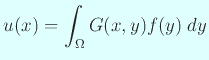
と表される。またより一般に
の解
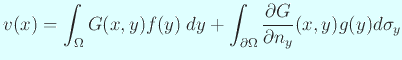
と表される。 Green 関数を用いると便利な状況が確かにある。
ところで、数値計算で、 境界値問題を解くために Green 関数を求めることは、 Green 関数を求める計算自身が境界値問題を解くことなので、 堂々巡りに近い、厳しくいうと余計な回り道をしている感が否めない。
桂田 祐史