20.1 渦糸の力学系

2次元の渦糸系と呼ばれる力学系について、 岡本 [71] を読み (10ページもない)、 必要な勉強を行ない、紹介されている数値実験を追試する。

$N$ 個の渦糸からなる渦糸系の方程式は、 $k$ 番目の渦糸の座標を $(x_k(t),y_k(t))$ として、

$$\frac{\D x_k}{\D t}=\sum_{j=1\atop j\ne k}^N \frac{-\Gamma_j}{2\pi} \frac{y_k(t)-y_j(t)}{(x_k(t)-x_j(t))^2+(y_k(t)-y_j(t))^2}$$

$$\frac{\D y_k}{\D t}=\sum_{j=1\atop j\ne k}^N \frac{\Gamma_j}{2\pi} \frac{x_k(t)-x_j(t)}{(x_k(t)-x_j(t))^2+(y_k(t)-y_j(t))^2}$$

という微分方程式で表わされる。これは Hamilton 力学系であり、 数学的にはきれいな方程式であると言える。

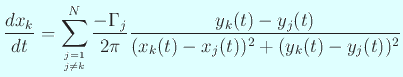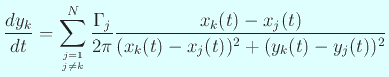中木達幸 (http://www.ofc.kyushu-u.ac.jp/kyokandb/data/html/0002/KMAT00066.html) という人の研究にも注目。

稲垣亜希子・栗田智昭・田中賢史 [69] という卒業研究レポートがあり、

「2次元渦糸系のシミュレーション」

に Java アプレットが用意されている。

(ひとり言) 竜巻とか、台風の藤原効果とか、渦関係で面白そうな話題は色々あるが、 チャレンジするには適度に簡単化しないと困難だと思われる。 渦糸はかなり大胆な簡単化だけれど、それでも自明でない構造を持っているらしい。