3.8 船見俊哉「Shortley-Weller 近似による Poisson 方程式のシミュレーション」

差分法では、問題を考える領域 $\Omega$ を座標軸に平行な等間隔の格子で分割し、 格子線の交点である格子点における関数値を考察の対象とする。 領域 $\Omega$ が、座標軸に平行な辺を持つ長方形領域の場合は、 境界上に格子点を容易に配置できて都合が良い。

しかし円盤領域のような境界が曲がっている場合は、困難が生じる。 問題を考える領域を変数変換で長方形の形をした領域に写像して、 後者の領域で差分法を実行することが良く行われている。

Shortley-Weller 近似では、 等間隔刻みをあきらめた不等間隔差分近似を用いる。

$u$ が $(x,y)$ の近傍で $C^4$ 級である場合、 通常の2階中心差分近似では

$$\Laplacian u(x,y) -\left( \frac{u(x+h_x,y)-2u(x,y)+u(x-h_x,y)}{h_x^2} +\frac{u(x,y+h_y)-2u(x,y)+u(x,y-h_y)}{h_y^2} \right)$$

$$=O(h_x^2+h_y^2) h\to 0$$

という2次精度を示す式が容易に得られる。 一方、Shortley-Weller近似の場合は2次精度を示す式は得られない。 その代り

$$\Laplacian u(x,y) - \biggl( \frac{1}{h_e+h_w} \left( \frac{u(x+h_e,y)-u(x,y)}{h_e}-\frac{u(x,y)-u(x-h_2,y)}{h_w} \right)$$

$$+ \frac{1}{h_n+h_s} \left( \frac{u(x,y+h_n)-u(x,y)}{h_n}-\frac{u(x,y)-u(x,y-h_s)}{h_s} \right) \biggr) =O(...)$$

のような式が得られる。 それにもかかわらず、差分解の精度は2次精度になる (Yamamoto [15], Matsunaga-Yamamoto [16])。

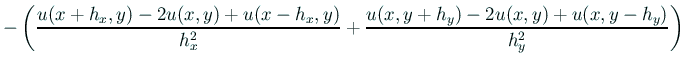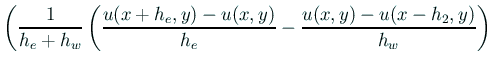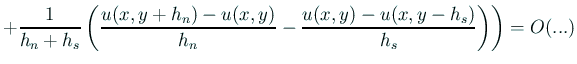この結果は非常に興味深い。 これを齊藤宣一氏にずっと以前に教示されたことがきっかけになって、 桂田研の卒業研究で多くの学生に Shortley-Weller 近似に取り組んでもらった (金子[21], 久保田 [20], 濱 [19], 嵯峨野 [20])。 ところが、 それらの研究で対象としたのは、熱方程式、波動方程式に対する陽解法であった。 そうなった理由の一つは、陰解法のプログラムの作成を敬遠したことにある (要するに、実際にどのようにプログラムを作れば良いのかが分からなかった)。 今回の船見君の研究では、 陰解法のプログラム開発に真正面から取り組んでもらった。 紆余曲折あったが見事に成功した。 数値実験の結果は、確かに2次精度の差分解が得られているように思われる。

この研究で分かったことを利用すれば、 熱方程式の陰解法プログラムや、 L字型領域における問題を解くプログラムも作成できると思われる。 理論的な問題も色々残されているのではないだろうか (Nuemann境界値問題や熱方程式の差分スキームの安定性など)。

船見君の研究により、Shortley-Weller 近似は、 勧めやすい研究テーマとなった。