Next: 3.8 船見俊哉「Shortley-Weller 近似による Poisson Up: 3 2017年度卒業研究 Previous: 3.6 高原智輝「ピタゴラスの鍛冶屋でのエピソードの検証」
田所君はサッカーが趣味で、変化球のシミュレーションの話を振ったら、 興味を持ったので、 以前から注目していた野地 [13] を読むことをすすめた。 [13] では、野球のカーブが念頭にあったようだが、 田所君はサッカーボールのシュートのシミュレーションを目標においた。 [13] のトレースを続けていく途中でタイムアップとなった。
実は [13] において、 実際の野球に相当する条件での計算は出来ていない。 田所君の数値計算も、実際のサッカーボールのシュートに相当する条件での 計算は実現できていない (Reynolds数が大き過ぎる)。 リアルな問題を扱うのは大変である。 その点を打破するには、 安定して計算するための工夫を導入する必要があると思われる。 挑戦者が現れることを望む。
この研究の過程で、以下のことを学んだ。
ボールの直径は
![]() ,
大人のシュートスピードは
,
大人のシュートスピードは
![]() ,
回転の速さは毎秒
,
回転の速さは毎秒 ![]() 回転という数値を採用した。
回転という数値を採用した。
無次元化するため、代表的な長さ ![]() として
として ![]() ,
代表的速さとして
,
代表的速さとして ![]() を採用した。
Reynolds数は
を採用した。
Reynolds数は
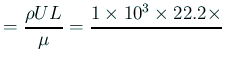
以下では無次元化した方程式のみを示す。
実際には、ボールが移動するので、流体の占める領域は時間変化するが、 それでは計算が面倒なので、ボールの位置を原点に取る座標系を採用する。 それは慣性系なので見かけの力は現れない。
また、有限要素法では無限領域を扱うことは難しいので、 ボールから十分離れたところに仮想的な境界を設け、 それに囲まれた有界な領域で計算を行う。
(![]() から空気が流入する。
から空気が流入する。![]() から流出する。)
から流出する。)
流速
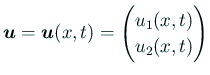 ,
圧力
,
圧力 ![]() を求める。
を求める。
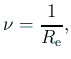 | ||
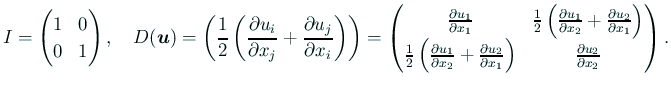 |
(5) は通常「応力境界条件」と呼ばれる。
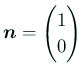 であるから、成分表示すると
であるから、成分表示すると
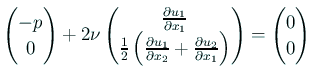
整理すると
|
(
|
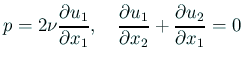 ( (
|
(6) は通常「すべり境界条件」と呼ばれる。
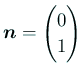 ,
,
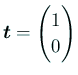 であるから、成分表示すると
であるから、成分表示すると
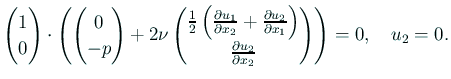
整理すると
|
(
|
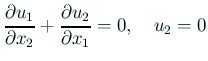 ( (
|
(書きかけ)
桂田 祐史