3.6 高原智輝「ピタゴラスの鍛冶屋でのエピソードの検証」

ボエティウス (Anicius Manlius Torquatus Severinus Boethius, 480-524) は著書の『音楽綱要』（De institutione musica、『音楽教程』とも） の中で、、、 この話は有名であるが、弦の話と異なり、納得が行かない。

実際、ウィキペディアのピタゴラスの項には次のように記されている。

ウィキペディア(2018/2/16)から引用

ある日鍛冶屋の前を通ったピタゴラスは、 作業場の何人かの職人が打っているハンマーの音が共鳴して、 快い協和音を発していることに気が付いた。中に入って調べてみると、 ハンマーの音程は、その重量と関係があった。 そこには五本のハンマーがあったが、 四本の鎚の重さは「12 : 9 : 8 : 6」 の単純な数比の関係にあることが解ったのである。 単純な比になっていない他の1本のハンマーだけは、鳴らすと不協和音がした （しかし実際にはこの原理は楽器の弦の長さの比率においては正しいが、 金槌の重さには当てはまらない）。

弦の振動では、周波数は弦の長さに反比例することが比較的簡単に分かる。 そのため、弦の音についてピタゴラスが発見したと信じられていることは容易に 納得できる。 しかし、3次元の物体の振動の場合はどうだろうか。 それは弦の場合より複雑であり、どのように振動するかは簡単には解けない。 しかし例えば波動方程式

$$\frac{\rd^2 u}{\rd t^2}=c^2\Laplacian u,\quad \Laplacian=\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}+\frac{\rd^2}{\rd z^2}$$

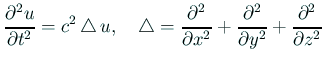
に従うことを仮定すると、 変数変換の議論を用いて、 周波数 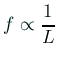$f$ が長さ $L$ に反比例すること( $f\propto\dfrac{1}{L}$ ) を導ける。 槌の質量 $m$ は長さの3乗に比例するので、

$$f\propto\frac{1}{m^{1/3}}.$$

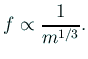
あるいは、槌の振動は波動方程式に従うものではないのかもしれない。 例えば棒の振動は

$$\frac{\rd^2 u}{\rd t^2}=-c^2\frac{\rd^4 u}{\rd x^4},$$

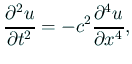
薄い板の振動は

$$\frac{\rd^2 u}{\rd t^2}=-c^2\Laplacian^2 u,\quad \Laplacian=\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}$$

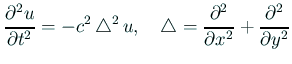
に従うことが知られている。このような場合も、 上と同様のテクニックで、 周波数は長さの2乗に反比例する ( 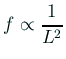$f\propto\dfrac{1}{L^2}$ ) ことが導ける。 槌の質量 $m$ は長さの3乗に比例するので、

$$f\propto\frac{1}{m^{2/3}}$$

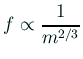
となる。

同じ材質で出来た、相似形の金槌を探すのは難しいと思ったが、 高原君は釣りの浮きを見つけてきて、実際に測定した。