2.4 解の係数を求める

私は、信号処理とフーリエ変換という授業で次のように教えています。

直交系による展開の係数

　直交系 $\{X_n\}_{n\in\mathbb{N}}$ によって、関数 $f$ が

$$f(x)=\sum_{n=1}^\infty a_n X_n(x)$$

と展開されているとき、

$$a_n=\frac{(f,X_n)}{(X_n,X_n)}$$

が成り立つ。ただし $(\cdot,\cdot)$ は次式で定義される関数の内積である。

$$(f,g)=\int_0^1 f(x)\overline{g(x)}\Dx.$$

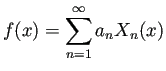
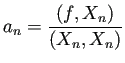
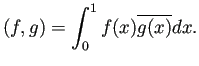
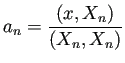$f(x)=x$ の場合は、 $a_n=\dfrac{(x,X_n)}{(X_n,X_n)}$, $X_n(x)=\sin\lambda_n x$ であるから、 次のコードで計算できる。

Clear[a]
a[n_]:=a[n]=Integrate[x Sin[lambda[n] x], {x,0,1}]/Integrate[Sin[lambda[n] x]^2, {x,0,1}]

Table[a[n],{n,10}]

次のような結果を返す。

Out[] = {0.729175, -0.156164, 0.0613973, -0.0321584, 0.0196707,
         -0.0132429, 0.00951282, -0.00715998, 0.0055821, -0.00447313}

[1] p. 58 の表7.2と見比べてみよう。