Next: D..5 問題 5 Up: D..4 問題4 Previous: D..4 問題4
典型的な極値問題。微分係数が 0 となる点を求めて、 そこで Hesse 行列を求めて、符号 (正値?負値?不定符号?) を調べて、 極値かどうかを判定する。
In[1] := f[x_,y_]:=2x^3+6x y^2-2x
In[2] := jf[x_,y_]:=D[f[a,b],{{a,b}}]/.{a->x,b->y}
In[3] := jf[x,y]
In[4] := H[x_,y_]:=D[f[a,b],{{a,b},2}]/.{a->x,b->y}
In[5] := MatrixForm[H[x,y]]
|
![\begin{jremark}
\begin{enumerate}[(1)]
\item
単に $f$ のヤコビ行列を...
...�に計算出来ることに注目しよう。
\qed
\end{enumerate}\end{jremark}](img313.gif)
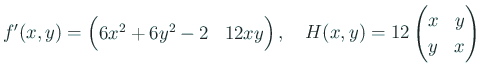
停留点を求めて、Hesse行列を計算して、符号を調べてみる。
In[6] := sp=Solve[jf[x,y]=={0,0},{x,y}]
In[7] := H[x,y]/. sp
In[8] := Eigenvalues[H[x,y]]/. sp
In[9] := f[x,y]/.sp
|
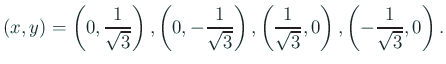
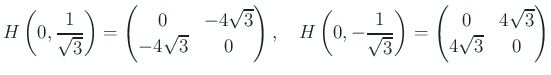
はともに (固有値が
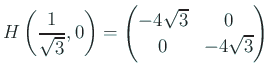
の固有値は
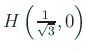 は負値である。
ゆえに、
は負値である。
ゆえに、
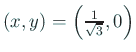 で
で 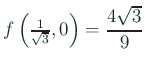 .
.
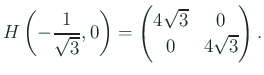
の固有値は
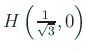 は正値である。
ゆえに、
は正値である。
ゆえに、
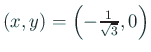 で
で 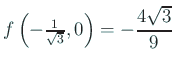 .
.
![]() での接平面は
での接平面は
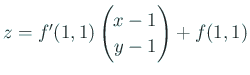 であるから、
であるから、
In[10] := Simplify[jf[1,1].{x-1,y-1}+f[1,1]]
|
桂田 祐史