5.16 不定積分、定積分

不定積分は Integrate[式, 変数], 定積分は Integrate[式, 変数の範囲] とします。

Integrate[1/(1+x^2),x]	$\dsp\int \frac{1}{1+x^2}\Dx$
Integrate[1/(1+x^2),{x,0,1}]	$\dsp\int_0^1 \frac{1}{1+x^2} \Dx$
Integrate[E^(-x^2),{x,0,Infinity}]	$\dsp\int_0^\infty e^{-x^2}\Dx$

定積分の場合、数値積分版 NIntegrate[] もあります。 近似値しか計算できませんが、 Integrate[] では計算できないような定積分も扱えます。

NIntegrate[Sqrt[Sin[x]], {x,1,2}]
NIntegrate[Sqrt[Sin[x]], {x,1,2}, WorkingPrecision->50,AccuracyGoal->40]

文字定数を含んだ関数の積分をするとき、 その定数が正数であるとか、実数であるとか、 Mathematica に教えてやらないと計算出来ないこともあります。

  Assuming[a>0, Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}]

  Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}, Assumptions->{a>0}]

  Integrate[Exp[-x^2]Cos[2a x],{x,-Infinity,Infinity}, Assumptions->Im[a]==0]

これと少し似ている問題に、 z[u_]:=NIntegrate[Sqrt[1-Exp[-2*t]],{t,0,u}] のように、 NIntegrate[] を使って定義した関数を含む式を評価するときに、 積分範囲が数値として定まらないうちに評価してしまうと問題が生じる、 というものがあります。 こういう場合は、 z[u_?NumericQ]:=NIntegrate[Sqrt[1-Exp[-2*t]],{t,0,u}] のように定義すると、u が数値であるかどうか判定出来るまで、 z[] の評価が後回しにされて問題を回避出来る場合があるようです。

x[u_] = Exp[-u]
z[u_?NumericQ] := NIntegrate[Sqrt[1 - Exp[-2*t]], {t, 0, u}]
p[u_, v_] := {x[u]*Cos[v], x[u]*Sin[v], z[u]}
ParametricPlot3D[p[u, v], {u, 0, 3}, {v, 0, 2*Pi}]

(Mathematica のバージョンによっては、 ?NumericQ がなくても問題なく動きますが、 警告が表示されるバージョンもあります。)

限定的ですが、 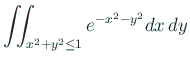$\dsp\dint_{x^2+y^2\le 1}e^{-x^2-y^2}\DxDy$ のような重積分も出来ます (重積分の計算については、誰かレポートを書いてくれないかな…)。

  Integrate[Exp[-x^2-y^2] Boole[x^2+y^2<=1], {x,-1,1}, {y,-1,1}]