H..3 Mathematica の間違える例

これも学生の発見。

高木貞治『解析概論』にある収束する広義積分

$$\int_0^\infty\frac{x}{1+x^6\sin^2 x}\Dx$$

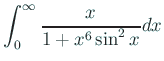
を、Mathematica が発散すると答える (もちろん Mathematica の間違い) ことを発見した (最新の Mathmatica 9 で試してみても， 「…の積分は $(0,\infty)$ で収束しません」と応答が返って来る)。

201x年7月某日のSNS

昨日の情報処理２で学生から質問あり。

レポート課題で、Mathematica に教科書の問題を解かせるなりして、 Mathematica が間違えた例を見つけて、その理由を考えてみなさい、 というのを出してあるのだけど (この課題は毎年出しているのですが、 最近はやってくれる人が少ないです)、その流れで

$$\int_0^\infty \frac{x}{1+x^6\sin^2 x}dx$$

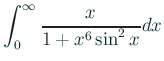
という広義積分について、本には (ちらと見たら高木貞治「解析概論」ぽかった…後で確認出来ました) 収束すると書いてあるけれど、Mathematicaは発散すると答えを出します、 これがMathematicaの間違えている例になるでしょうか、との質問。

忙しかったので、Mathematica おかしいみたいですね、時間がないのでまた今 度、 と言ったのですが、今日になって気がつきました。このちょっと難し目の積分、 どうやって計算するか、昨年研究発表を聴いたことがあるのでした。

大浦拓哉, ある非有界無限区間積分の高速高精度計算

http://www.kurims.kyoto-u.ac.jp/~ooura/papers/toda53a.pdf

被積分関数ぱっと見は分母に $x^6$ があって、遠方で小さくなりそうですが、 $\sin$ があるせいで、分母が $x=n\pi$ のところで $1$ になるので、 関数値自体は $n\pi$ になって全然小さくなってくれない。 というわけで積分の収束を証明するだけでも大変です。 上の論文には収束の確認は、Goursat と G. H. Hardy による、 とあります。 偉い人二人の名前が出て来る由緒正しい積分だったわけですね。 それが高木先生の解析概論に載っていた、と。

高木先生の放ったボールを学生がキャッチ。ちょっと楽しい出来事でした。

ちなみに、この収束証明もやさしくない広義積分、実は100万桁以上計算した、 というのが上の論文の内容です（かなりすごい）。