Next: D..6 問題6 Up: D..5 問題 5 Previous: D..5 問題 5
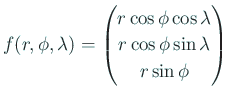
In[1] := f[r_,p_,l_]:={r Cos[p]Cos[l],r Cos[p]Sin[l], r Sin[p]}
In[2] := jf[a_,b_,c_]:=D[f[r,p,l],{{r,p,l}}] /. {r->a,p->b,l->c}
In[3] := MatrixForm[jf[r,p,l]]
In[4] := Det[jf[r,p,l]]
In[5] := Simplify[%]
|
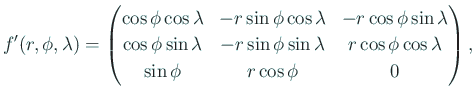
桂田 祐史