

Next: A..1.3 無理数性・超越性
Up: A..1 円周率の概念
Previous: A..1.1 円周率の定義
円周と直径の比として定義されたので、
「半径
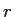
の円の円周は
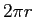
」
「半径
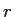
の円の面積は
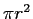
」
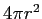 と体積
と体積
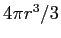 を発見し、
そのことを証明したことで非常に名高い)。
を発見し、
そのことを証明したことで非常に名高い)。
余談になりますが、
円周、円の面積、球の表面積、球の体積の
いずれにも 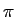 が (
が (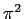 ,
, 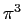 でなく) 生で現れるのは、
不思議と言えば不思議です
(2年生は、
後期に一般の
でなく) 生で現れるのは、
不思議と言えば不思議です
(2年生は、
後期に一般の 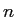 次元球の「体積」や「表面積」を学ぶ機会がありますが、
そのときにどうなるか、目を凝らして見て下さい)。
次元球の「体積」や「表面積」を学ぶ機会がありますが、
そのときにどうなるか、目を凝らして見て下さい)。


Next: A..1.3 無理数性・超越性
Up: A..1 円周率の概念
Previous: A..1.1 円周率の定義
桂田 祐史
2013-06-12
![]() が (
が (![]() ,
, ![]() でなく) 生で現れるのは、
不思議と言えば不思議です
(2年生は、
後期に一般の
でなく) 生で現れるのは、
不思議と言えば不思議です
(2年生は、
後期に一般の ![]() 次元球の「体積」や「表面積」を学ぶ機会がありますが、
そのときにどうなるか、目を凝らして見て下さい)。
次元球の「体積」や「表面積」を学ぶ機会がありますが、
そのときにどうなるか、目を凝らして見て下さい)。