自然対数の底 (Euler の数,
Napier の数とも言う) ![]() の計算で実践してみましょう。
の計算で実践してみましょう。
![]() は
は
![]() の
の ![]() における値なので、テイラー展開
における値なので、テイラー展開
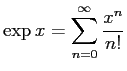 (
(に
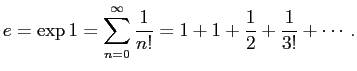
これを例えば 10 項まで足すと
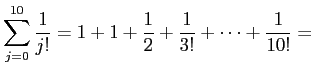
と (実は小数点以下第7位まで正しい)
さて、それでこの計算をどう実行するか。
和 ![]() の計算は前回やりました。
の計算は前回やりました。
| 復習: 和
|
|
s=0
for j=1 to n s=s+( next j |
これを参考に、
一般項
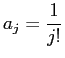 が漸化式
が漸化式
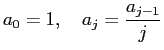
で与えられることを利用すると、 次のコードが得られます。
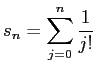 を
を |
REM 自然対数の底をテイラー級数で計算 N=10 REM a0, s0 LET A=1 LET S=A FOR J=1 TO N LET A=A/J LET S=S+A NEXT J PRINT S END |
問 色々な N に対する部分和を計算してみよう。 どうするのが良いか? (正解と言えるものはないかもしれないが、 工夫してみよう。)