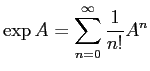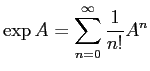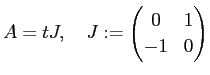

Next: A. 前回の後始末
Up: 2012年度情報処理II 第13回 MATLAB 体験
Previous: 2.3 絶対値最大の固有値を求める
締め切りは 7月20日(金) 18:00。Oh-o! Meiji レポートシステムを使って、
kadai13.pdf を提出する。
neumann.m を参考に、
行列の指数関数
を計算する関数 exponential() を作って下さい。
例えば
のとき、
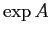 が何になるか調べて
(対馬先生のテキストの付録
http://nalab.mind.meiji.ac.jp/~tsushima/senkei.html の第9章の章末問
題2参照)、それを MATLAB の計算結果と比較しなさい
(
が何になるか調べて
(対馬先生のテキストの付録
http://nalab.mind.meiji.ac.jp/~tsushima/senkei.html の第9章の章末問
題2参照)、それを MATLAB の計算結果と比較しなさい
(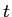 は適当に 1 つ 2 つ選べば良い。
は適当に 1 つ 2 つ選べば良い。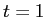 とか
とか 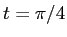 とか。)。
とか。)。


Next: A. 前回の後始末
Up: 2012年度情報処理II 第13回 MATLAB 体験
Previous: 2.3 絶対値最大の固有値を求める
桂田 祐史
2012-07-11