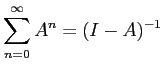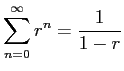

Next: 2.3 絶対値最大の固有値を求める
Up: 2.2 行列の等比級数
Previous: 2.2 行列の等比級数
Neumann 級数の (部分) 和
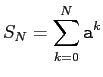 に
に
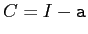 をかけた結果が単位行列に非常に近いことが分かります。
種明かしをすると、一般に
をかけた結果が単位行列に非常に近いことが分かります。
種明かしをすると、一般に
が成り立つからです。これは等比級数の和の公式
の行列への一般化です。


Next: 2.3 絶対値最大の固有値を求める
Up: 2.2 行列の等比級数
Previous: 2.2 行列の等比級数
桂田 祐史
2012-07-11
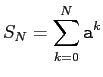 に
に
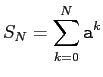 に
に
![]() をかけた結果が単位行列に非常に近いことが分かります。
種明かしをすると、一般に
をかけた結果が単位行列に非常に近いことが分かります。
種明かしをすると、一般に