

Next: 1.8.2 Newton 法の特徴
Up: 1.8 二分法 vs. Newton
Previous: 1.8 二分法 vs. Newton
- (i)
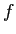 が微分可能でなくとも連続でありさえすれば適用できる。
が微分可能でなくとも連続でありさえすれば適用できる。
- (ii)
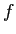 は
は 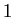 変数実数値関数でない場合は適用が難しい
(特に実数値であることはほとんど必要であると言ってよい)。
変数実数値関数でない場合は適用が難しい
(特に実数値であることはほとんど必要であると言ってよい)。
- (iii)
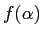 と
と 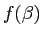 の符号が異なる
の符号が異なる 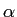 と
と 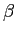 が
見つかっていれば、確実に近似解が求まる。
が
見つかっていれば、確実に近似解が求まる。
- (iv)
- 収束は遅い。
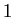 回の反復で
回の反復で 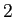 進法にして
進法にして 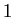 桁ずつ精度が改善されていく程度である。
桁ずつ精度が改善されていく程度である。
(例えば 10進1000桁 (2進3000桁以上) 求める場合を考えてみよう。)


Next: 1.8.2 Newton 法の特徴
Up: 1.8 二分法 vs. Newton
Previous: 1.8 二分法 vs. Newton
桂田 祐史
2012-05-30