自然対数の底 (Euler の数,
Napier の数とも言う) ![]() の計算で実践してみましょう。
の計算で実践してみましょう。
![]() は
は
![]() の
の ![]() における値なので、テイラー展開
における値なので、テイラー展開
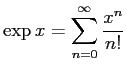
に
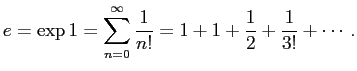
これを例えば 10 項まで足すと
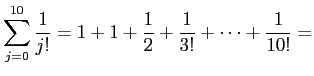
と (実は小数点以下第7位まで正しい)
さて、それでこの計算をどう実行するか。 和の計算は前回やりました。
| 復習: 和
|
|
s=0
for j=1 to n s=s+( next j |
これを参考に、
一般項
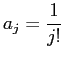 が漸化式
が漸化式
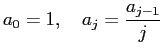
で与えられることを利用すると、 次のコードが得られます。
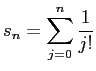 を
を |
REM 自然対数の底をテイラー級数で計算 N=10 REM a0, s0 LET A=1 LET S=A FOR J=1 TO N LET A=A/J LET S=S+A NEXT J PRINT S END |
問 色々な N に対する部分和を計算してみよう。 どうするのが良いか? (正解と言えるものはないかもしれないが、 工夫してみよう。)
| 表示する桁数の指定 | |||
例えば変数 S の値を小数点以下 10 位まで表示させるには、
PRINT USING という命令を利用して
なお、FMT$, REPEAT$() の $ は、 変数や関数が文字列である場合につける決まりになっている文字です。 |