一見漸化式と関係なさそうでも、 漸化式を用いて計算すると便利というものが結構あります。
例えば数列 ![]() の第
の第![]() 項から第
項から第![]() 項までの和
項までの和
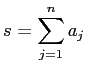 は、部分和
は、部分和
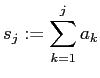
を導入すると、数列
あるいは
という漸化式で定義することができます。 例えば
|
s=0
for j=1 to n s=s+( next j print s |
REM squaresum.BAS REM 自然数の平方の和 INPUT PROMPT "Nを入力してください:": N S=0 FOR J=1 to N S=S+J^2 NEXT J PRINT S REM 知っている公式で値を計算して確認 PRINT N*(N+1)*(2*N+1)/6 END |