next up previous
Next: 3 課題7解説 Up: 2 課題6B解説 Previous: 2.2 AGM, 代表選手 Gauss-Legendre

2.3 参考: 色々な $ \arctan$ 公式を比較する

http://nalab.mind.meiji.ac.jp/~mk/syori2-2011/jouhousyori2-2011-06/node18.htmlで紹介した公式を比較してみるのも面白いです。

こういうのは実際に試してみて初めて分かることが多く、 挑戦できる腕力のある人は是非やってみることをお勧めします。

いくつかアドバイスをします。

(1)
たくさんの $ \arctan$ を計算するので、 $ \arctan$ の計算を副プログラム (関数またはサブルーチン) にすることを お勧めします。 次のサンプル・プログラムは、 piarctan.bas を外部副関数を使って計算するように書き換えたものです。 

REM piarctan2.bas --- ޡ쥴꡼饤ץ˥åĵǦФ׻
REM arctanεη׻ϳؿǤ뤳Ȥˤ
DECLARE EXTERNAL FUNCTION arctan
INPUT x
INPUT n
LET  s=arctan(x,n)
PRINT "arctan(x)";s
print "4";4*s
PRINT USING "ФȤκ=-%.###^^^^^^":4*s-PI
END

EXTERNAL FUNCTION arctan(x,n)
REM arctan x ε n ޤǷ׻
LET  f=-x*x
LET  t=x
LET  s=0
for j=1 to n
   LET  a=t/(2*j-1)
   LET  s=s+a
   LET  t=f*t
NEXT j
LET  arctan=s
END FUNCTION
(2)
級数の部分和 $ s_n(x)$ は、 $ n$ をどこまで大きく取れば十分な精度を持つのか？ 一般にはそれほど簡単ではありませんが、 今考えている $ \arctan$ の級数の場合は、 各項の絶対値が単調に減少する交代級数になるので、 次の Leibniz の定理によって簡単に見通しが立ちます ($ s_n$ の誤差は、次に足す項の絶対値 $ a_{n+1}$ 以下である)。
交代級数に関する Leibniz の定理
数列 $ \{a_n\}_{n\ge 1}$ は単調減少 ( $ a_1\ge a_2\ge \cdots$ ) で、 $ \dsp\lim_{n\to\infty}a_n=0$ を満たすとき、級数

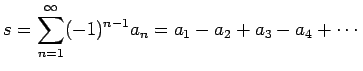
$\displaystyle s=\sum_{n=1}^\infty (-1)^{n-1}a_n =a_1-a_2+a_3-a_4+\cdots $

は収束する。第 $ n$ 部分和を $ s_n$ とすると、

$\displaystyle s_{2n}\le s\le s_{2n-1}$   $\displaystyle \mbox{($n\in\N$)}$$\displaystyle , $

$\displaystyle \left\vert s-s_n\right\vert\le a_{n+1}$   $\displaystyle \mbox{($n\in\N$)}$

が成り立つ。

次に掲げる結果は、 100桁程度の精度を得るために、 級数の和を何項加える必要があるか概算し、 実際にそれを実行するとどれくらいので精度になるかを計算したものです。

大体どれくらいか…

㡼
 205 ޤDzä׵٤ãޤ
 9.81E-101

ޥ 2
 71 ޤDzä׵٤ãޤ
 22 ޤDzä׵٤ãޤ
 1.20E-101

Gauss 3
 40 ޤDzä׵٤ãޤ
 29 ޤDzä׵٤ãޤ
 22 ޤDzä׵٤ãޤ
 1.23E-102

Gauss 4
 32 ޤDzä׵٤ãޤ
 29 ޤDzä׵٤ãޤ
 22 ޤDzä׵٤ãޤ
 21 ޤDzä׵٤ãޤ
 1.09E-103

Gauss 9
 14 ޤDzä׵٤ãޤ
 13 ޤDzä׵٤ãޤ
 13 ޤDzä׵٤ãޤ
 12 ޤDzä׵٤ãޤ
 12 ޤDzä׵٤ãޤ
 11 ޤDzä׵٤ãޤ
 11 ޤDzä׵٤ãޤ
 10 ޤDzä׵٤ãޤ
 10 ޤDzä׵٤ãޤ
 7.45E-106

ͺ4
 30 ޤDzä׵٤ãޤ
 29 ޤDzä׵٤ãޤ
 22 ޤDzä׵٤ãޤ
 11 ޤDzä׵٤ãޤ
 7.29E-105

Stormer4
 29 ޤDzä׵٤ãޤ
 22 ޤDzä׵٤ãޤ
 18 ޤDzä׵٤ãޤ
 13 ޤDzä׵٤ãޤ
 7.73E-104

この結果をどう分析すべきか… 書きたくてむずむずするけれど、 誰かにやって欲しいので書きません。

(一言だけ： Gauss は色々大理論を作った偉い人だけど、 こういう計算も大好きだったのが良く分かります。)

next up previous
Next: 3 課題7解説 Up: 2 課題6B解説 Previous: 2.2 AGM, 代表選手 Gauss-Legendre
桂田 祐史
2012-04-30