| (3) | 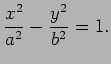 |
| 「2定点からの距離の差が一定である点の軌跡は双曲線である」の解析幾何的証明 |
|
2定点を
を移項して
両辺を平方して
整理して
再び両辺を平方して
移項して
割り算して
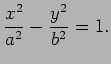
|
(![[*]](crossref.png) ) で与えられる双曲線には、
有名なパラメーター表示が二つある。
一つは
) で与えられる双曲線には、
有名なパラメーター表示が二つある。
一つは
| (4) |
| (5) | 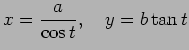 |
a = 3; b = 2;
ParametricPlot[{{a Cosh[t], b Sinh[t]},
{-a Cosh[t], b Sinh[t]}},
{t, -3, 3},
PlotRange -> {{-10*a, 10*a}, {-10*b, 10*b}},
AspectRatio -> b/a]
|
a=3; b=2; eps=0.1;
g1=ParametricPlot[{a/Cos[t],b Tan[t]},{t,-Pi/2+eps,Pi/2-eps}];
g2=ParametricPlot[{a/Cos[t],b Tan[t]},{t,Pi/2+eps,3*Pi/2-eps}];
Show[g1,g2,PlotRange->All,AxesOrigin->0]
|