| (1) | 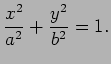 |
| 「2定点からの距離の和が一定である点の軌跡は楕円である」の解析幾何的証明 |
|
2定点を
を移項して
両辺を平方して
消去、移項、整理して
再び両辺を平方して
移項して
割り算して
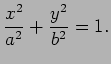
|
円
![]() を
を ![]() 軸方向に
軸方向に
![]() 倍したものと考えると、
倍したものと考えると、
| (2) |
set parametric set size ratio -1 a=3 b=2 plot [0:2*pi] a*cos(t),b*sin(t) |
a=3; b=2; ParametricPlot[{a Cos[t],b Sin[t]},{t,0,2Pi}]
|