Next: 2.1.0.1 余談 Up: 2 プログラム作成実習 Previous: 2 プログラム作成実習
次のような Laplace 方程式の境界値問題を考えよう。
![]() を
を
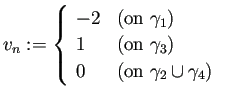
次のLaplace方程式の境界値問題を考える。
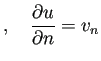 on
on
これは実は2次元非圧縮ポテンシャル流の速度ポテンシャル ![]() を求める問題である。
速度場を
を求める問題である。
速度場を ![]() とすると、境界上で
とすると、境界上で
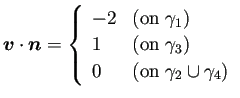
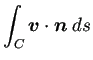
上の境界値は、
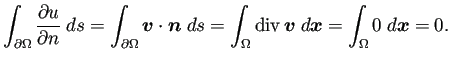
この問題を解くプログラムを1から作成しても良いが、 Laplace方程式やPoisson方程式のプログラムを探して、 それを書き換えることでプログラムを作成してみよう。
(Poisson方程式
![]() で
で ![]() とすると、
Laplace方程式であることに注意。)
とすると、
Laplace方程式であることに注意。)
Poisson方程式用のプログラム poisson-kikuchi.edp は公開してある。それを叩き台にしてみる。
curl -O https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi.edp cp poisson-kikuchi.edp my-laplace.edp |
この my-laplace.edp を書き換えて行こう。
これは Poisson 方程式のDirichlet-Neumann境界値問題を解くプログラムであるが、
![]() とすれば Laplace 方程式となる。
とすれば Laplace 方程式となる。
+on(Gamma1,) を削除すると Dirichlet境界条件はなくすことができる。
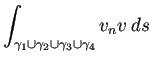 は、各パートにわけて与えればよい。例えば
-int1d(Th,gamma1)(g21*v)-int1d(Th,gamma3)(g23*v)
とする。
は、各パートにわけて与えればよい。例えば
-int1d(Th,gamma1)(g21*v)-int1d(Th,gamma3)(g23*v)
とする。![]() と
と ![]() では
では ![]() なので、
積分を計算する必要はない。
なので、
積分を計算する必要はない。
![]() ,
, ![]() での
での ![]() を g21, g23
で与えることにした。
を g21, g23
で与えることにした。
解 ![]() の等高線は、いわゆる等ポテンシャル線であるが、
その gradient は速度場
の等高線は、いわゆる等ポテンシャル線であるが、
その gradient は速度場 ![]() なので、
それを描くと良いかもしれない。
なので、
それを描くと良いかもしれない。
// ベクトル場の表示 Vh u1,u2; u1=dx(u); u2=dy(u); plot([u1,u2],wait=1); |
解答例
// my-laplace.edp
// https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi.edp を元にした
// 菊地文雄, 有限要素法概説, サイエンス社
border gamma1(t=0,pi/6) { x=cos(t); y=sin(t); }
border gamma2(t=pi/6,pi) { x=cos(t); y=sin(t); }
border gamma3(t=pi,4*pi/3) { x=cos(t); y=sin(t); }
border gamma4(t=4*pi/3,2*pi) { x=cos(t); y=sin(t); }
int m=10;
mesh Th = buildmesh(gamma1(m)+gamma2(5*m)+gamma3(2*m)+gamma4(4*m));
plot(Th,wait=true,ps="Th.eps");
savemesh(Th,"Th.msh");
fespace Vh(Th,P1);
Vh u,v;
func f=0;
func g21=-2;
func g23=1;
solve Poisson(u,v)=
int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
-int2d(Th)(f*v)
-int1d(Th,gamma1)(g21*v)
-int1d(Th,gamma3)(g23*v);
plot(u,wait=1,ps="my-laplace.eps");
//3次元鳥瞰図
//real [int] levels =0.0:0.01:1.0;
//plot(u,dim=3,viso=levels,fill=true,wait=true);
// ベクトル場の表示
Vh u1,u2;
u1=dx(u);
u2=dy(u);
plot([u1,u2],wait=1);
|