Next: 3 法のコードを作る Up: 法のプログラムを作って実験 Previous: 1 はじめに
時間について![]() 法で差分近似した方程式は
法で差分近似した方程式は
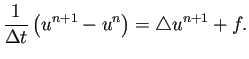 |
(6) |
これに対する弱形式は以下の通り。
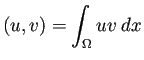 ,
,
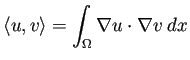 ,
,
![$ [g_2,v]=\dsp\int_{\Gamma_2}g_2 v\;\D\sigma$](img19.png) ,
,
FreeFem++ で対応するコードは
| heatB.edp 内の problem |
problem heat(u,v,init=n)= int2d(Th)(u*v)-int2d(Th)(uold*v) +int2d(Th)(tau*(dx(u)*dx(v)+dy(u)*dy(v))) -int2d(Th)(tau*f*v)-int1d(Th,2,3)(tau*g2*v) +on(1,4,u=g1);(ラベル |
このコードが弱形式 (7) の実現であることは読み取ろう。
