Next: 2 後退Euler法のコードを読む Up: 法のプログラムを作って実験 Previous: 法のプログラムを作って実験
(内部での熱発生を考慮した) 熱方程式の初期値境界値問題
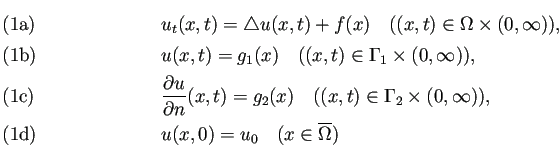 |
![]() 法では、
法では、
![]() を満たす
を満たす![]() を取って、
微分方程式
を取って、
微分方程式
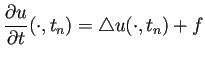 を
を
| (3) |
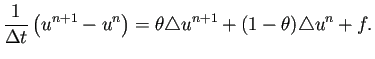 |
(5) |
後退Euler法については、弱形式とサンプル・プログラム
heatB.edp を与えておいた。
![]() 法については、弱形式はあるが、プログラムがない。
このような場合にプログラムを作る作業はよくあるタイプの作業である。
法については、弱形式はあるが、プログラムがない。
このような場合にプログラムを作る作業はよくあるタイプの作業である。
| heatB.edp を叩き台にして heatT.edp を作る |
curl -O https://m-katsurada.sakura.ne.jp/program/fem/heatB.edp cp heatB.edp heatT.edp |