2.10.5 DE 公式

[端点の特異性くらい何でもない]

$$I=\int_{-1}^1 \sqrt{1-x^2} \Dx=\frac{\pi}{2}, \quad J=\int_{-1}^1\frac{1}{\sqrt{1-x^2}} \Dx=\pi.$$

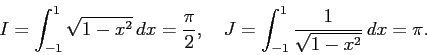
誤差の表

test1 (sqrt(1-x^2) の積分)
 h=1.000000, I_h=       1.7125198292703636, I_h-I=1.417235e-01
 h=0.500000, I_h=       1.5709101233831164, I_h-I=1.137966e-04
 h=0.250000, I_h=       1.5707963267997540, I_h-I=4.857448e-12
 h=0.125000, I_h=       1.5707963267948970, I_h-I=4.440892e-16
 h=0.062500, I_h=       1.5707963267948970, I_h-I=4.440892e-16
 h=0.031250, I_h=       1.5707963267948954, I_h-I=-1.110223e-15
 h=0.015625, I_h=       1.5707963267948979, I_h-I=1.332268e-15
 h=0.007812, I_h=       1.5707963267948957, I_h-I=-8.881784e-16
 h=0.003906, I_h=       1.5707963267948959, I_h-I=-6.661338e-16
 h=0.001953, I_h=       1.5707963267948954, I_h-I=-1.110223e-15
test2 (1/sqrt(1-x^2) の積分)
 h=1.000000, I_h=       3.1435079763395435, I_h-I=1.915323e-03
 h=0.500000, I_h=       3.1415926717394895, I_h-I=1.814970e-08
 h=0.250000, I_h=       3.1415926194518016, I_h-I=-3.413799e-08
 h=0.125000, I_h=       3.1415926318228000, I_h-I=-2.176699e-08
 h=0.062500, I_h=       3.1415926343278695, I_h-I=-1.926192e-08
 h=0.031250, I_h=       3.1415926326210664, I_h-I=-2.096873e-08
 h=0.015625, I_h=       3.1415926323669550, I_h-I=-2.122284e-08
 h=0.007812, I_h=       3.1415926327540102, I_h-I=-2.083578e-08
 h=0.003906, I_h=       3.1415926312582481, I_h-I=-2.233155e-08
 h=0.001953, I_h=       3.1415926319069580, I_h-I=-2.168284e-08