1. 数値積分についての概説

よく知られているように積分の計算はむつかしい。定積分を数値的に近似計算 することを数値積分という。

この文書では、主に $1$ 次元の定積分

$$I=\int_a^b f(x) \Dx\quad\mbox{($-\infty\le a<b\le \infty$)}$$

の計算法について説明する。

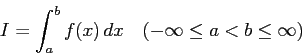
微分については、合成関数の微分法により、例えば初等関数の導 関数は初等関数になるなど、機械的に計算できてしまうことが多い。特に 高速微分法 (自動微分法とも言う) という効率的なアルゴ リズムの存在が知られている。

多次元の積分に関しては、紙と鉛筆の計算においては、Fubini の定理

$$\dint_{A\times B} f(x,y) \Dx\Dy=\int_B \left(\int_A f(x,y) \Dx\right)\Dy$$

に基づく累次積分への帰着が使われることが多いが、この手順をそのまま応用 して $1$ 次元の数値積分を繰り返すのは良くないとされている (らしい)。

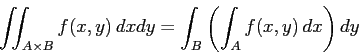
(『応用数理』に多次元の数値積分についての論説があったように思う。 探し出して参考文献表に加え、できれば内容の紹介を書くこと。)