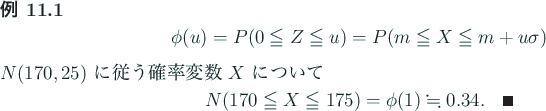Next: 確率密度関数表の自前での印刷 Up: 11 正規分布 Previous: 11.1.0.3 確率密度関数のグラフを眺める
標準正規分布 ![]() に従う確率変数
に従う確率変数 ![]() を考える。その確率密度関数
は
を考える。その確率密度関数
は ![]() ,
,
![]() として
として
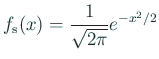
残念ながら
![]() の原始関数は求められないので、
の原始関数は求められないので、
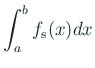
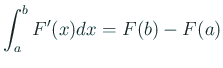 は使えない。
は使えない。
そこで、従来は数表を用意するのが普通であった。 例えば教科書の p. 55 にある数表は
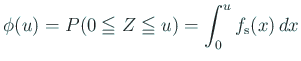
また被積分関数が偶関数であるから ![]() は奇関数である。
は奇関数である。
数表があるとき、公式 (6), (7) を用いれば、 確率は簡単に計算できる。例えば
最近は電卓でも計算できるようになっているし、プログラミング言語のライ ブラリィ関数にも用意されている。
| 余談: erf() | |
|
プログラミング言語 C の数学関数ライブラリィには、
erf(), erfc() という関数が用意されていることが多い
(Mathematica にもあるみたい)。
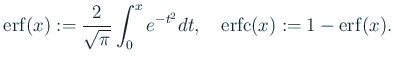
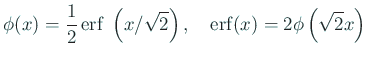
(老婆心: erfc() を用意するのは桁落ち対策でしょうね。) |