Next: 1.2 の Fourier 係数 Up: 1 Fourier級数の部分和のグラフを描く Previous: 1 Fourier級数の部分和のグラフを描く
![]() の Fourier 級数展開を求めてみよう。
の Fourier 級数展開を求めてみよう。
![]() は偶関数であるから、
は偶関数であるから、![]() はすぐ分かる
(実際、
はすぐ分かる
(実際、
![]() は奇関数であるから
は奇関数であるから
![]() で積分すると 0
)。
で積分すると 0
)。
![]() は偶関数で、
は偶関数で、![]() では
では ![]() に等しいので、
に等しいので、
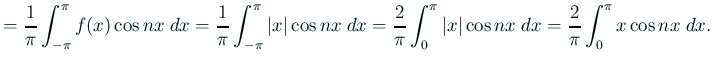 |
![]() のときは、
のときは、
![$\displaystyle a_0=\frac{2}{\pi}\int_0^\pi x\;\Dx
=\frac{2}{\pi}\cdot\left[\frac{x^2}{2}\right]_0^\pi=\pi.
$](img31.gif)
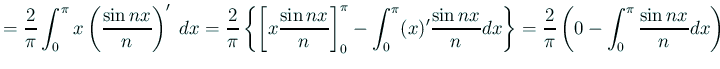 | ||
![$\displaystyle =\frac{2}{\pi}\left[\frac{\cos nx}{n^2}\right]_{0}^\pi =\frac{2}{...
...text{($n$\ は奇数)} \\ [1ex] 0& \text{($n$\ は偶数)}. \end{array} \right.$](img34.gif) |
=\frac{\pi}{2}
-\sum_{n\ge 1\atop \text{$n$は偶数}}\df...
...t(\frac{\cos x}{1^2}+\frac{\cos
3x}{3^2}
+\frac{\cos 5x}{5^2}+\cdots\right).
$](img35.gif)
f[x_]:=Abs[x]
fp[x_]:=Abs[Mod[x,2Pi,-Pi]]
Plot[fp[x],{x,-3Pi,3Pi}]
|
1/Pi Integrate[f[x]Cos[n x],{x,-Pi,Pi}]
|
a[n_]:=Simplify[1/Pi Integrate[f[x]Cos[n x],{x,-Pi,Pi}],Element[n,Integers]]
a[n]
Table[a[n],{n,0,10}]
|
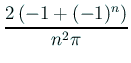 が得られる。
が得られる。
桂田 祐史