次の(1)が非常に重要である。
例年それを間違えてナンセンスなレポートを提出する人が少なくない。
- (1)
-
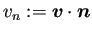 は
は
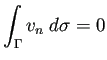 を満たしている必要がある。実際、Gaussの発散定理と非圧縮性の仮定から
を満たしている必要がある。実際、Gaussの発散定理と非圧縮性の仮定から
サンプルプログラムでは、
円盤領域
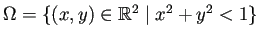 なので
なので
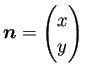 (ここは良く考えること).
また一様流
(ここは良く考えること).
また一様流
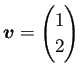 であったので、
であったので、
としてある。(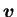 が
が 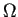 で定数関数なので)
で定数関数なので)
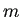 であるから、
当然
であるから、
当然
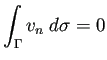 も成り立つ。
(そうでない場合は、きちんと計算して
も成り立つ。
(そうでない場合は、きちんと計算して
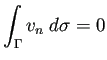 が成り立つことを確かめる必要がある。)
が成り立つことを確かめる必要がある。)
- (2)
- 湧き出しや吸い込み、点渦など、特異点が
 内にあるような問題は、
この方法では解くことが出来ない。
内にあるような問題は、
この方法では解くことが出来ない。
質問されたことへの回答
- 境界値
 を、if を用いた場合分を含む関数としたいが、
FreeFem++ がプログラムを受け付けてくれません
→ 例えば
を、if を用いた場合分を含む関数としたいが、
FreeFem++ がプログラムを受け付けてくれません
→ 例えば
- (a)
- 弱形式には複数の int1d() が指定できるので、
境界を分割して、
その各部分ごとに(場合分けを含まない)境界値を与えるようにプログラムを書く。
- (b)
- 例えば (x>1 && y>0) のような式は、条件が成り立つならば
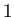 , 成り立たないならば0という値を持つので、ifを使わずに、
式だけで場合分けを含む関数が記述できる。
, 成り立たないならば0という値を持つので、ifを使わずに、
式だけで場合分けを含む関数が記述できる。
桂田 祐史
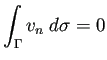 を満たしている必要がある。実際、Gaussの発散定理と非圧縮性の仮定から
を満たしている必要がある。実際、Gaussの発散定理と非圧縮性の仮定から
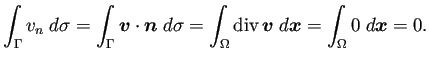
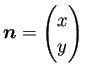 (ここは良く考えること).
また一様流
(ここは良く考えること).
また一様流
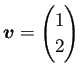 であったので、
であったので、
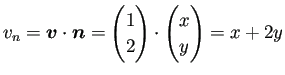
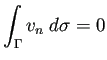 も成り立つ。
(そうでない場合は、きちんと計算して
も成り立つ。
(そうでない場合は、きちんと計算して
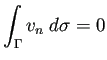 が成り立つことを確かめる必要がある。)
が成り立つことを確かめる必要がある。)