課題2

2次元非圧縮ポテンシャル流の定常流で、流体の占める領域 $\Omega$ と、 その境界 $\Gamma=\rd\Omega$ での流速の法線成分 $v_n:=\bm{v} \cdot\bm{n}$ が分かっている場合に、速度ポテンシャル $\phi$、 流れ関数 $\psi$ を計算して、等ポテンシャル線、流線、速度場を可視化せよ。 領域$\Omega$と境界値(流速の法線成分) $v_n$ は、 自分で興味のあるもの、自分の都合の良いものを選んで良い (後の注意を読んでおくこと)。

$\phi$ は、ポテンシャル問題 (ここでは Laplace方程式のNeumann境界値問題)

$$\Laplacian\phi=0 \Omega$$ (1)

$$\frac{\rd\phi}{\rd\bm{n}}=v_n \Gamma$$ (2)

の解である。

ポテンシャル問題 (1), (2)を解いて、等ポテンシャル線と速度場 $\bm{v}$ を求めるサンプル・プログラム potential2d-v0.edp を公開してある。

potential2d-v0.edp は、ターミナルで次のようにして入手する

curl -O http://nalab.mind.meiji.ac.jp/~mk/complex2/potential2d-v0.edp

大筋は、 $\Omega$ と $v_n$ を自分が決めたものにするようにプログラムを書き換えれば良い。 (弱形式は変更する必要がない。) 自由度は高いので、 工夫・遊び心発揮を期待する。

(過去の例では、円を楕円にするような(一見)安直な選択があったが、 そういう人の多くは、 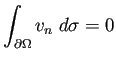$\dsp\int_{\rd\Omega}v_n\; \D\sigma=0$ を満たす $v_n$ が見つけられなかったりしていた。)

流線の書き方には色々なやり方がある (一つくらいノーヒントの問を入れておくことにする)。 選んだ問題によっては、分かりやすい図が描けるように調整が必要な場合もある。