次の (1) と (2) を行うこと。
どちらも正則関数の定める流れを可視化し説明する、 という問題である。
- (1)
- §3.14「流れの合成」 (講義ノート「複素関数と流体力学」
[1] の§4.3
「基本的な流れの重ね合わせ」に対応している) から3つの流れを選んで、
等ポテンシャル線、流線、
ベクトル場を適当に (流れの様子が良く分かるように) 可視化し、
流れがどのようなものか説明せよ (特に流速に注意すること)。
特徴的な流線における流れ関数の値が分かるように説明すること。
[どのように取り組むか] 一様流、
湧き出しのサンプル・プログラム (Mathematica) は
で公開してある。
それらは講義内容と対応するように書かれていて、
それを解読すれば要領は分かるはず。
細かいところは各々の流れに合うように直す必要がある。
- (2)
-
自分で思いつく正則関数を3つ以上試し
(「 係数だけを変えて数合わせ」ではなく、
なるべく授業の例と「違う」ものを選ぶこと。
三角関数・指数関数 (例えば
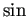 と
と 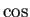 ,
,
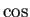 と
と 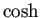 は本質的には同じであり、
同じものを選ぶのはつまらない)、
1次分数変換
は本質的には同じであり、
同じものを選ぶのはつまらない)、
1次分数変換
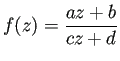 など、
色々な関数を知っているはず。そのうちの2つを選んで、
それを複素速度ポテンシャルとする流れについて、等ポテンシャル線、
流線、ベクトル場を適切に可視化し、それをもとにどういう流れであるか説明する。
など、
色々な関数を知っているはず。そのうちの2つを選んで、
それを複素速度ポテンシャルとする流れについて、等ポテンシャル線、
流線、ベクトル場を適切に可視化し、それをもとにどういう流れであるか説明する。
(2022/6/7追記)
ベクトル場のプロットについて質問があったので、
http://nalab.mind.meiji.ac.jp/~mk/lecture/applied-complex-function-2022/vectorplot/
という説明を書きました。
桂田 祐史
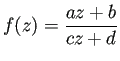 など、
色々な関数を知っているはず。そのうちの2つを選んで、
それを複素速度ポテンシャルとする流れについて、等ポテンシャル線、
流線、ベクトル場を適切に可視化し、それをもとにどういう流れであるか説明する。
など、
色々な関数を知っているはず。そのうちの2つを選んで、
それを複素速度ポテンシャルとする流れについて、等ポテンシャル線、
流線、ベクトル場を適切に可視化し、それをもとにどういう流れであるか説明する。