Next: B..2.2 C言語のプログラム例 Up: B..2 1次元でイントロ Previous: B..2 1次元でイントロ
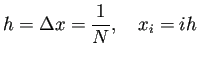 (
(
| (B.10) | 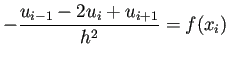 ( (
| |
| (B.11) | ||
| (B.12) | 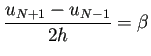 |
結果として次の連立1次方程式が得られる:
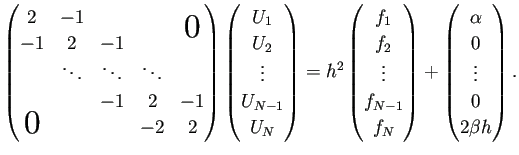
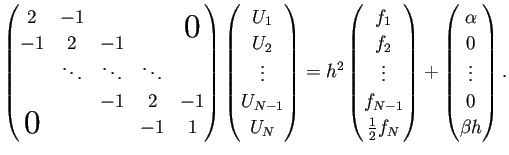
この係数行列は既約優対角行列なので、正則である。
ゆえに連立1次方程式は一意的な解を持つ。
また、この係数行列は、対角線とその両隣り以外は 0 とになっている、
いわゆる三重対角行列であり (連立1次方程式自体は三項方程式と呼ばれる)、
Gaussの消去法で効率的に(![]() の計算量で) 解くことが出来る。
の計算量で) 解くことが出来る。