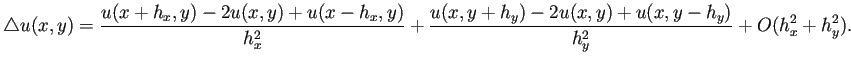B..1 基本的な考え方

差分法 (finite difference method, FDM) では、次の2つの考え方を用いる。

常微分方程式の初期値問題に対する Euler 法, Runge-Kutta 法などを学んだことがあれば、理解しやすいであろう。

(B.1)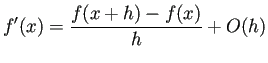

$\displaystyle f'(x)=\frac{f(x+h)-f(x)}{h}+O(h)$ ( $h\to 0$ ) $\displaystyle .$

(B.2)

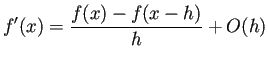$\displaystyle f'(x)=\frac{f(x)-f(x-h)}{h}+O(h)$ ( $h\to 0$ ) $\displaystyle .$

(B.3)

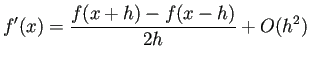$\displaystyle f'(x)=\frac{f(x+h)-f(x-h)}{2h}+O(h^2)$ ( $h\to 0$ ) $\displaystyle .$

(B.4)

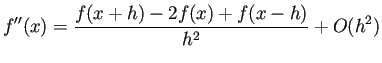$\displaystyle f''(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+O(h^2)$ ( $h\to 0$ ) $\displaystyle .$

(B.5)

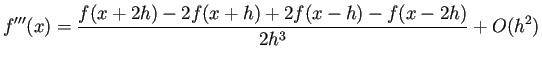$\displaystyle f'''(x)=\frac{f(x+2h)-2f(x+h)+2f(x-h)-f(x-2h)}{2h^3} +O(h^2)$ ( $h\to 0$ ) $\displaystyle .$

(B.6)

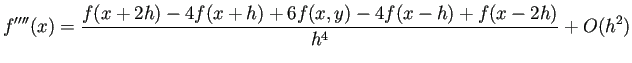$\displaystyle f''''(x)=\frac{f(x+2h)-4f(x+h)+6f(x,y)-4f(x-h)+f(x-2h)}{h^4}+O(h^2)$ ( $h\to 0$ ) $\displaystyle .$

多変数関数の偏導関数はこれらを適当に組み合わせて近似する。例えば

$\displaystyle \Laplacian u(x,y) =\frac{u(x+h_x,y)-2u(x,y)+u(x-h_x,y)}{h_x^2} +\frac{u(x,y+h_y)-2u(x,y)+u(x,y-h_y)}{h_y^2} +O(h_x^2+h_y^2).$

桂田祐史