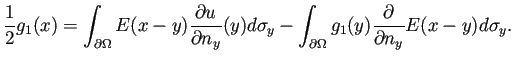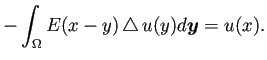Green の第2積分公式
を利用して、次のGreen の第3積分公式を得る
(証明の詳細は略するが、
関数論の Cauchy の積分公式の証明のように、
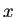 を中心とする球を除いた領域で Green の公式を適用してから、
球の半径を 0 に近づける。詳しくは桂田[3]の§3.5を見よ。)。
を中心とする球を除いた領域で Green の公式を適用してから、
球の半径を 0 に近づける。詳しくは桂田[3]の§3.5を見よ。)。
(
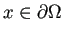 の場合は左辺第3項は主値積分である。)
の場合は左辺第3項は主値積分である。)
- (a)
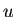 が
が
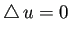 を満たすならば、
を満たすならば、
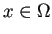 に対して、
に対して、
すなわち、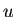 が調和関数であるとき、
が調和関数であるとき、
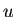 ,
,
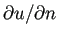 の
の 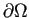 での値が分かれば、
での値が分かれば、
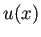 の値がこの式で求まることになる
(正則関数の Cauchy の積分公式に似ていて、使いでのある公式)。
境界条件から半分は分かっているので、
もう半分求めれば良いことになる。
の値がこの式で求まることになる
(正則関数の Cauchy の積分公式に似ていて、使いでのある公式)。
境界条件から半分は分かっているので、
もう半分求めれば良いことになる。
以下は細かい話になるが: 例えば
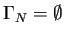 のとき、
のとき、
これから 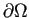 上で
上で
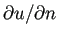 を求めることが出来る。
を求めることが出来る。
- (b)
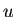 が
が 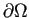 の近傍で 0 ならば、
の近傍で 0 ならば、
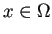 に対して、
に対して、
この事実を超関数解釈すると
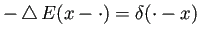 となる。
となる。
桂田 祐史
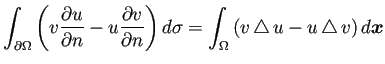
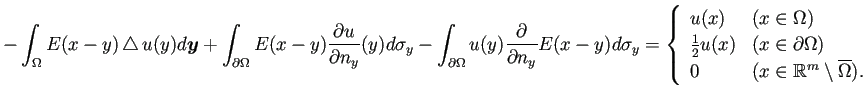
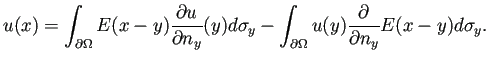
![]() のとき、
のとき、