3 数値積分の実例

ターミナルから

curl -O http://nalab.mind.meiji.ac.jp/~mk/complex2/prog20190715.tar.gz
tar xzf prog20190715.tar.gz
cd prog20190715
make

なめらかな関数の積分

$$I=\int_0^1 e^x \;\Dx$$

を複合中点公式、複合台形公式、複合Simpson公式で求めた場合の誤差が gnuplot example2.gp で図示される。

図: $I=\dsp\int_0^1 e^x\;dx$ を中点公式、台形公式、Simpson公式で計 算したときの誤差

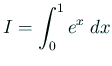
端点でなめらかさのない関数の積分

$$I=\int_0^1 \sqrt{1-x^2\;}\Dx$$

を複合中点公式、複合台形公式、複合Simpson公式で求めた場合の誤差が gnuplot example3.gp で図示される。

図: $I=\dsp\int_0^1\sqrt{1-x^2}\;dx$ を中点公式、台形公式、Simpson 公式で計算したときの誤差

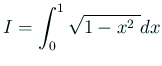
なめらかな周期関数の一周期積分

$$I=\int_0^{2\pi}\frac{\Dx}{2+\cos x}$$

を複合中点公式、複合台形公式、複合Simpson公式で求めた場合の誤差が gnuplot example4.gp で図示される。 誤差が非常に速く減少するので、数値を見た方が良いかもしれない。 それには ./example4 あるいは

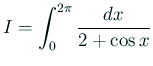
ターミナルで

cat ex4.data
#   N       I-M_N           I-T_N         I-S_N
    2    4.860061e-01  -5.611915e-01  -1.259323e+00
    4    3.720712e-02  -3.759270e-02   1.369402e-01
    8    1.927779e-04  -1.927882e-04   1.227385e-02
   16    5.122576e-09  -5.122576e-09   6.425590e-05
   32    8.881784e-16   4.440892e-16   1.707525e-09
   64    4.440892e-16  -1.776357e-15   8.881784e-16
  128   -1.776357e-15  -4.440892e-16  -4.440892e-16
  256   -3.996803e-15   3.108624e-15  -1.332268e-15
  512   -8.881784e-16   8.881784e-16  -1.332268e-15
 1024   -5.773160e-15  -3.996803e-15  -4.440892e-16
 2048   -5.329071e-15   8.881784e-15  -4.884981e-15
 4096    1.554312e-14  -3.108624e-15  -4.440892e-16
 8192   -1.421085e-14   2.220446e-15   9.325873e-15
16384   -1.643130e-14   3.108624e-15  -8.437695e-15
32768    4.440892e-15   4.574119e-14  -9.769963e-15
65536    2.664535e-14   3.108624e-15   1.820766e-14

図: $I=\dsp\int_0^{2\pi}\frac{1}{2+\cos x}\;dx$ を中点公式, 台形公式, Simpson公式で計算したときの誤差

$x\to\pm\infty$ での減衰が十分速い $\mathbb{R}$ 上の解析関数の積分として、 有名な確率積分

$$I=\int_{-\infty}^\infty e^{-x^2}\;\Dx$$

を台形公式

$$I_{h,N}=h\sum_{n=-N}^N f(nh)$$

で求めた場合の誤差は次のようにして表示できる。

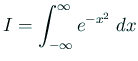
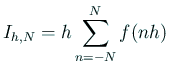
ターミナルで

./example5
確率積分の台形則による数値積分
 N       h                  T               I-T
 6	1	   1.772637204826652  -1.833539e-04
12	0.5	   1.772453850905516  -2.220446e-16
24	0.25	   1.772453850905516  -4.440892e-16