Next: この文書について... Up: 課題2 (もしかすると二つ出して、選択問題にするかも) Previous: 課題2 (もしかすると二つ出して、選択問題にするかも)
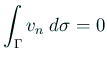 を満たしている必要がある。
実際、Gaussの発散定理と非圧縮性の仮定から
を満たしている必要がある。
実際、Gaussの発散定理と非圧縮性の仮定から
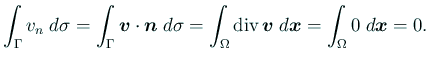
サンプルプログラムでは、 円盤領域
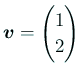 であったので、
であったので、
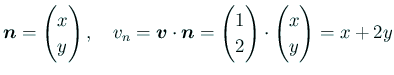
としてある。
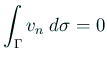 も成り立つ。
も成り立つ。
| potential2d-v0.edp |
1 // potential2d-v0.edp
2 // http://nalab.mind.meiji.ac.jp/~mk/complex2/potential2d-v0.edp
3 // 2次元非圧縮ポテンシャル流
4 // 速度ポテンシャル,速度を求め、等ポテンシャル線, 速度場を描く
5
6 border Gamma(t=0,2*pi) { x = cos(t); y = sin(t); } // 円盤領域
7 int m=40;
8 mesh Th=buildmesh(Gamma(m));
9 plot(Th, wait=1, ps="Th.eps");
10
11 fespace Vh(Th,P1);
12 Vh phi, v, v1, v2;
13 func Vn=x+2*y; // Ωが単位円で, V=(1,2) のとき V・n=x+2y
14
15 // 速度ポテンシャルφを求め、その等高線 (等ポテンシャル線) を描く
16 solve Laplace(phi,v) =
17 int2d(Th)(dx(phi)*dx(v)+dy(phi)*dy(v))
18 -int1d(Th,Gamma)(Vn*v);
19 plot(phi,ps="contourpotential.eps",wait=1);
20
21 // ベクトル場 (v1,v2)=∇φ を描く (ちょっと雑なやり方)
22 v1=dx(phi);
23 v2=dy(phi);
24 plot([v1,v2],ps="vectorfield.eps",wait=1);
25
26 // 等ポテンシャル線とベクトル場を同時に描く
27 plot([v1,v2],phi,ps="both.eps", wait=1);
|