2.1.0.1 Riemann による解の存在証明のあらすじ

境界条件 $u=g_1$ (on $\rd\Omega$ ) を満たす $u$ のうちで

$$J[u]=\dint_\Omega\left(u_x^2+u_y^2\right)\DxDy$$   (この $J$ を Dirichlet 積分と呼ぶ)

を最小にするものは、 $\Laplacian u=0$ を満たす。 この事実を Dirichlet の原理と呼ぶ。 実際、$v$ を $v=0$ (on $\rd\Omega$ ) を満たす任意の関数とするとき、

$$f(t):=J[u+t v]$$   ( $t\in\mathbb{R}$ )

は $t=0$ で最小となる (なぜならば、$u+t v$ も同じ境界条件を満たすので、 最小性の仮定から $J[u+t v]\ge J[u]$ . これを $f$ で言い換えると、 $f(t)\ge f(0)$ . これは $f$ が $t=0$ で最小になることを意味する。)。 ところで

$$f(t)=J[u]+2t\dint_\Omega\left(u_x v_x+u_y v_y\right)\DxDy +t^2\dint_\Omega\left(v_x^2+v_y^2\right)\DxDy$$

であるから、$f$ は2次関数であり、$t=0$ で最小となるためには

   $1$ 次の係数$$\quad \dint_\Omega\left(u_x v_x+u_y v_y\right)\DxDy=0$$

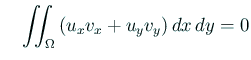
が必要十分である。Green の積分公式² を適用して

$$\dint_\Omega(u_{xx}+u_{vv})v\;\DxDy=0.$$

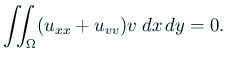
これが任意の $v$ について成り立つことから、 $\Laplacian u=u_{xx}+ u_{yy}=0$ .

以上の議論から、 $J[u]$ を最小にするような $u$ を見出せば問題が解決することが分かる。 $J$ は常に $J\ge 0$ を満たすので、$J$ が下に有界でありることは明らかで、 従って $J$ の下限が存在する。 Riemann は、 (この下限は最小値であるから) 最小値を与える $u$ が存在する、と議論したのだが、 Weierstrass は「下限は最小値である」ことに疑義を示した (「数学解析」を学んだ人は、 いかにも Weierstrass がツッコミそうなところと思うかも)。 $\qedsymbol$

残念ながら若くして亡くなった Riemann は、 Weierstrass の批判に答えることが出来なかった。 この論法による完全な証明は、 約 50 年後 (1900年頃) に D. Hilbert が解決するまで持ち越された。

本当は、Dirichlet の原理は、 C. F. Gauss (1777-1855) がルーツで、 物理学の世界ではすでに知られていた考え方で、 それを Riemann が純粋数学に応用したのだ、という見方をする人もいる。