Next: 2.1.3 Rungeの現象があるので Up: 2.1 補間多項式 Previous: 2.1.1 定義と一意存在
![]() を大きくすると「良い」補間多項式が得られそうに思えるかもしれないが、
それは誤解である。
を大きくすると「良い」補間多項式が得られそうに思えるかもしれないが、
それは誤解である。
標本点を等間隔に取って ![]() を大きくすると、
を大きくすると、![]() は
は ![]() と
似ても似つかないものになることがある
(Rungeの現象と呼ばれている)。
と
似ても似つかないものになることがある
(Rungeの現象と呼ばれている)。
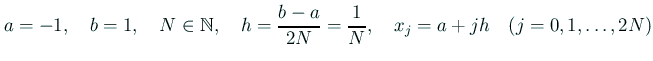
とする。実際に関数
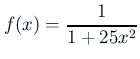
の補間多項式を求めてグラフを描いてみよう。
/*
* runge.c --- 等間隔標本点の補間多項式はポシャるという Runge の現象
* 参考: 森正武, 数値解析, 共立出版 (1973, 第2版 2002).
* gcc runge.c ; ./a.out > runge.data
* gnuplot> f(x)=1/(1+25*x*x)
* gnuplot> plot [-1:1] [-1:1] "runge.data" with linespoints, f(x)
* gnuplot> plot [-1:1] [-1:10] "runge.data" with linespoints, f(x)
*
* ここでは Lagrange 補間多項式として計算している。
*/
#include <stdio.h>
#include <stdlib.h>
/* [-1,1] での等間隔標本点がうまく行かないことで有名な関数 */
double f(double x)
{
return 1.0 / (1.0 + 25.0 * x * x);
}
/* Lagrange 補間係数 */
double L(double x, int k, int N, double xv[])
{
int j;
double t = 1;
for (j = -N; j <= N; j++)
if (j != k)
t *= (x - xv[j+N]) / (xv[k+N] - xv[j+N]);
return t;
}
/* Lagrange 補間公式 */
double fn(double x, int N, double xv[], double fv[])
{
int k;
double s = 0;
for (k = -N; k <= N; k++)
s += fv[k+N] * L(x, k, N, xv);
return s;
}
int main(void)
{
int j, N, nn;
double h;
double *xv, *fv;
N = 10;
xv = malloc(sizeof(double) * (2 * N + 1)); // エラーチェックさぼり
fv = malloc(sizeof(double) * (2 * N + 1)); // 同上
h = 1.0 / N;
for (j = -N; j <= N; j++) {
xv[j + N] = j * h;
fv[j + N] = f(xv[j + N]);
}
nn = 200;
h = 2.0 / nn;
printf("%g %g\n", -1.0, fn(-1.0, N, xv, fv));
for (j = 1; j <= nn; j++)
printf("%g %g\n", -1.0 + j * h, fn(-1.0 + j * h, N, xv, fv));
}
|
$ cc -o runge runge.c $ ./runge > runge.dat $ gnuplot gnuplot> f(x)=1/(1+25*x*x) gnuplot> plot [-1:1] [-1:1] "runge.dat" with linespoints,f(x) gnuplot> plot [-1:1] [-1:10] "runge.dat" with linespoints,f(x) |
グラフを見ると、区間の中央部分では、そこそこ近似できているが、
中央から離れるとずれが大きくなり、
端の近くでははなはだしい差が生じている。
これは標本点の個数を増やしても改善されず、
むしろ悪化する。 ![]()
上の ![]() は多くのテキストの例に採用されている。
大人しい関数と言って良いと思われる。
そういう関数の等間隔標本点による補間多項式の近似がうまく行かないのは、
不思議な感じがするかもしれない (私は最初知ったとき、とても驚きましたし、
色々と理解した今でも不思議に感じます)。
は多くのテキストの例に採用されている。
大人しい関数と言って良いと思われる。
そういう関数の等間隔標本点による補間多項式の近似がうまく行かないのは、
不思議な感じがするかもしれない (私は最初知ったとき、とても驚きましたし、
色々と理解した今でも不思議に感じます)。
桂田 祐史